2 Mapas coropléticos en R

De forma reciente, la información georreferenciada y los Sistemas de Información Geográfica (SIG) se han vuelto instrumentos de primer orden para el análisis y la presentación de fenómenos asociados al territorO. Por ejemplo, los Tableros de la Universidad Johns Hopkins sobre la pandemia por COVID19, o los del Gobierno de México y CentroGeo han estado constantemente en los medios de comunicación.

En este capítulo señalamos algunas de las características básicas de los datos y datos espaciales; además, buscamos brindar algunos elementos generales que te permitan familiarizarte con ese tipo de información y representarla gráficamente para usarla para en el analisis de fenómenos socioterritoriales.

2.1 Datos y datos espaciales

Los datos son valores, números o registros originados a partir de un proceso de recolección y procesamiento. Sirven para diversos propósitos, tales como el análisis científico y la toma de decisiones. Los datos se originan a partir de mediciones de conjuntos de objetos de la realidad. En estadística, ese conjunto de objetos de los que nos interesa saber ciertas cosas es denominado población y la información de sus rasgos o características es denominada variable o atributo. Así, las variables son medidas o características de los elementos que conforman la población. Si quieres explorar un poco y ampliar tus nociones de qué es un dato, puedes visitar esta entrada de Wikipedia o esta de Economipedia.

Las variables pueden ser medidas o información sobre cualidades de los objetos (por ejemplo, de una persona si está vacunada o no, si está enferma o sana) o bien, medidas o información sobre cantidades o elementos numéricos (por ejemplo, de una persona interesaría saber el número de dosis de una vacuna recibida, su edad) y las llamamos respectivamente variables cualitativas y variables cuantitativas.

Un tipo particular de datos son lo que denominamos datos espaciales o datos georeferenciados. Cuando utilizamos el apelativo “espaciales” o “georeferenciados” estamos diciendo con ello que dichos datos refieren un punto específico sobre la superficie terrestre. El proceso de referenciar geográficamente un dato es complejo pues remite a problemas sobre la forma de la Tierra y de su representación bidimencional a través de proyecciones cartográficas. Recomendamos revisar este material de Antonio Vazquez Brust donde se abunda sobre este problema.

Los datos espaciales se caracterizan por poseer tres componentes: localización, atributos y tiempo, aunque éste último no siempre aparece en todos los tipos de datos espaciales. Hay otro aspecto relacionado con la información espacial denominado calidad del dato geoespacial, que se refiere a que nuestro conjunto de información cumpla los requisitos necesarios para satisfacer la necesidad para la que se recabó, es decir, que sea útil para resolver la pregunta que motivó su recolección o uso.

La realidad es continua y compleja, además, muchos fenómenos tienen un referente territorial, es decir, se desarrollan y ocurren en un determinado lugar. Los datos espaciales implican un esfuerzo de abstracción, es decir, de simplificación de la realidad, a esto se le suele denominar a veces modelo espacial (Olaya 2020). Este proceso de abstracción consiste en “reducir o dividir esta continuidad en entidades numéricas discretas, observables y susceptibles de medición matemática” (así, un dato espacial podría definirse como la) “observación de una variable asociada a una localización del espacio geográfico” (Chasco 2003, 17). De forma general, es posible dividir los modelos de representación espacial de la realidad en dos tipos: ráster y vectorial.

1. Datos vectoriales: es una forma de representación de la realidad que consiste en el uso ya sea de puntos, líneas o polígonos (llamados a veces “primitivas”) para recoger ciertos aspectos de la realidad. ¿A través de qué primitiva podrías representar un camino? ¿Cuál para representar los límites de la localidad donde resides? Quizá podrías representar una vialidad a través de líneas, por un lado, y la representación de los límites administrativos de una región, a través de polígonos, por otro.
   
2. Datos ráster: es un modelo de representación espacial que “se basa en una división sistemática del espacio, la cual cubre todo este, caracterizándolo como un conjunto de unidades elementales” a los que se llama pixeles (Olaya 2020: Modelos de representación) . Por ejemplo, pueden ser imágenes del territorio provenientes de instrumentos ópticos (cámaras, sensores, aunqe no se limitan a ellos) e incluso el propio usuario puede definir dicha representación.³

Una definición mucho más cuidadosa de datos ráster y vectoriales puede encontrarse en el libro de Víctor Olaya sobre sistemas de información geográfica donde trata los tipos de datos espaciales.

Los ejemplos y ejercicios aquí desarrollado utilizan información espacial de tipo vectorial. Diversos formatos sirven para almacenar información de tipo vectorial, tales como Shape, GeoJSON (Geográphical JavaScript Object Notation), GeoPackage o KML (Keyhole Markup Language). No obstante, los shapefiles son aún los más comunes.

Los archivos vectoriales de tipo SHP fueron originalmente desarrollados por ESRI, empresa dedicada a la cosultoría de fenómenos territoriales, aunque hoy día se usan extensamente prácticamente en cualquier ámbito de interés científico donde se involucre el territorio. Almacenar información vectorial en un archivo SHP implica usar en realidad, al menos, tres archivos diferentes:

1. Archivo con extensión .shp: es un archivo que almacena las entidades espaciales representadas ya sea a través de puntos, líneas o polígonos.
   
2. Archivo con extensión .dbf (data base file): contiene los atributos o variables de cada objeto espacial contenido en el archivo shp.
   
3. Archivo con extensión .shx (index file): archivo que sirve de vínculo entre los dos previos.

Estos tres archivos son los mínimos indispensables para poder trabajar con modelos vectoriales de información, sin embargo no son los únicos que encontrarás cuando descargues archivos de este tipo. ⁴ Los tres archivos deben llevar el mismo nombre y deben estar en el mismo directorio (carpeta) para poder funcionar correctamente, es decir, para que sean leídos por el sistema de cómputo.

Para que comprendas lo anterior a cabalidad, descarga el conjunto de información espacial que usaremos aquí. Tras descomprimir la carpeta verás que contiene, entre otros, los siguientes archivos:

1. covid_zmvm.shp
2. covid_zmvm.shx
3. covid_zmvm.dbf

---

Ejercicio

Revisa la carpeta descargada y descomprimida para responder a lo siguiente:

1. ¿Cuáles son las extensiones de los otros archivos del mismo nombre?

2. ¿Para qué sirven esos archivos?

---

Como señalamos, la exploración y representación de la información a través de mapas es no sólo una herramienta muy útil y potente, sino que se ha popularizado en los últimos años gracias no sólo a la mayor disponibilidad de información georreferenciada, sino a la facilidad con la que ahora se puede acceder a software para la gestión y manipulación de este tipo de información.

Existen diversas herramientas informáticas para el análisis de información espacial y su representación, entre ellos se cuentan las alternativas de ESRI: ArcGIS y ArcMap. No obstante, el precio de una licencia individual es considerablemente alto, convirtiéndolos en inaccesibles a las mayorías. Una alternativa cada vez más popular es el programa QGIS, una iniciativa de software libre de la Fundación OSGeo, o bien, otra posibilidad también libre es el intuitivo programa de Luc Anselin (Universidad de Chicago, Centro para las Ciencias de Datos Espaciales) y su equipo para iniciarse en el análisis espacial, GeoDa.

Además, la popularidad del software R como plataforma de análisis ha hecho que múltiples entusiastas programadoras interesadas en el análisis espacial desarrollaran paquetes enfocados en el tratamiento y representación de datos espaciales para esta plataforma. Además de ser libre, entre las ventajas que tiene usar R como Sistema de Información Goegráfica y como espacio para el tratamiento de datos espaciales, es que se puede tener no sólo pleno control de la edición de los materiales cartográficos, sino que permite un entorno de trabajo integrado. En el resto de este capítulo se presenta de forma introductoria la manera en que R, a través de algunos paquetes, se puede convertir en un espacio de edición de mapas.

2.2 Los paquetes

Para la elaboración de mapas en R requeriremos de los siguientes paquetes:

• sf: un paquete útil para manejar datos espaciales de tipo vectorial.
  
• tmap: permite crear mapas para visualizar cómo una variable se distribuye en el espacio.
  
• RColorBrewer: proporciona esquemas de colores para los mapas, basados en el trabajo de la cartógrafa estadounidense Cynthia Brewer.
  
• cartogram: permite elaborar un tipo de mapa llamado cartograma.

Instala estos paquetes como es usual:

install.packages(c("sf","tmap", "RColorBrewer", "cartogram" ))

Para cargar los paquetes recién instalados procedemos como es habitual:

library(sf)
library(tmap)
library(RColorBrewer)
library(cartogram)

2.3 Carga de la base de datos geográfica

La base de datos a utilizar es la misma que la del capítulo anterior, es decir, información de la primera ola de la pandemia por COVID19 en la Zona Metropolitana del Valle de México, en el centro de México, y algunas variables sociodemográficas y económicas de sus unidades espaciales; no obstante, ahora haremos uso del shapefile (recuerda, al menos tres archivos: .shp, .dbf y .shx). Debemos cargar la geometría asociada a nuestra base de datos, el archivo con extensión .shp, para ello hay que usar la función st_read() del paquete sf:

zmvm_cov_sf <-sf::st_read("base de datos\\covid_zmvm shp\\covid_zmvm.shp")

## Reading layer `covid_zmvm' from data source 
##   `C:\repos\Analisis-de-datos-espaciales\base de datos\covid_zmvm shp\covid_zmvm.shp' 
##   using driver `ESRI Shapefile'
## Simple feature collection with 76 features and 57 fields
## Geometry type: MULTIPOLYGON
## Dimension:     XY
## Bounding box:  xmin: 2745632 ymin: 774927.1 xmax: 2855437 ymax: 899488.5
## Projected CRS: Lambert_Conformal_Conic

Nota cómo aparece en tu entorno de trabajo el objeto solicitado, zmvm_cov_sf, ¿logras ver qué tipo de objeto es? Tener esto en mente te ayudará a comprender que dependiendo del tipo de objeto con el que interactuas en R habrá determinadas funciones que podrás usar. Así como hay algunas funciones que nos permiten familiarizarnos con los objetos de tipo dataframe, las hay para el caso de los objetos de tipo sf (simple features). La función st_crs() nos ofrece información sobre el sistema de coordenadas de referencia, coordinate reference system (crs), de la capa cargada:

sf::st_crs(zmvm_cov_sf)

## Coordinate Reference System:
##   User input: Lambert_Conformal_Conic 
##   wkt:
## PROJCRS["Lambert_Conformal_Conic",
##     BASEGEOGCRS["GCS_GRS_1980_IUGG_1980",
##         DATUM["D_unknown",
##             ELLIPSOID["GRS80",6378137,298.257222101,
##                 LENGTHUNIT["metre",1,
##                     ID["EPSG",9001]]]],
##         PRIMEM["Greenwich",0,
##             ANGLEUNIT["Degree",0.0174532925199433]]],
##     CONVERSION["unnamed",
##         METHOD["Lambert Conic Conformal (2SP)",
##             ID["EPSG",9802]],
##         PARAMETER["Latitude of false origin",12,
##             ANGLEUNIT["Degree",0.0174532925199433],
##             ID["EPSG",8821]],
##         PARAMETER["Longitude of false origin",-102,
##             ANGLEUNIT["Degree",0.0174532925199433],
##             ID["EPSG",8822]],
##         PARAMETER["Latitude of 1st standard parallel",17.5,
##             ANGLEUNIT["Degree",0.0174532925199433],
##             ID["EPSG",8823]],
##         PARAMETER["Latitude of 2nd standard parallel",29.5,
##             ANGLEUNIT["Degree",0.0174532925199433],
##             ID["EPSG",8824]],
##         PARAMETER["Easting at false origin",2500000,
##             LENGTHUNIT["metre",1],
##             ID["EPSG",8826]],
##         PARAMETER["Northing at false origin",0,
##             LENGTHUNIT["metre",1],
##             ID["EPSG",8827]]],
##     CS[Cartesian,2],
##         AXIS["(E)",east,
##             ORDER[1],
##             LENGTHUNIT["metre",1,
##                 ID["EPSG",9001]]],
##         AXIS["(N)",north,
##             ORDER[2],
##             LENGTHUNIT["metre",1,
##                 ID["EPSG",9001]]]]

De la enorme cantidad de información que aparece en tu consola, nota cómo la proyección de nuestra base de datos geográfica es la Cónica Conforme de Labert, Lambert_Conformal_Conic. En su Introducción ligera a los SIG el equipo de QGIS señala que “Con la ayuda de Sistemas de Referencia de Coordenadas (SRC) cualquier punto de la tierra puede ser definido por tres números denominados coordenadas. En general, los CRS se pueden dividir en sistemas de referencia de coordenadas proyectados (también denominados Cartesianos o sistemas de referencia de coordenadas rectangulares) y sistemas de referencia de coordenadas geográficos”.

Los sistemas proyectados están basados en determinada representación de los sistemas geográficos. La selección de un adecuado CRS asegura que las características deseadas se representen en el mapa de forma precisa. Existen varios elementos que diferencian los Sistema de Coordenadas Proyectadas (PCS) y los Sistema de coordenadas geográficas (GCS). Mientras que un “sistema de coordenadas geográficas es un método para describir la posición de una ubicación geográfica en la superficie de la Tierra utilizando mediciones esféricas de latitud y longitud (además de que) se trata de mediciones de los ángulos (en grados) desde el centro de la Tierra hasta un punto en la superficie de la Tierra representada como una esfera”, tal y como se señala en la ayuda del sitio de internet de la aplicación de sistemas de información geográfica (SIG), ArcMap (ESRI 2023b).

En tanto, “un sistema de coordenadas proyectadas se define sobre una superficie plana de dos dimensiones. A diferencia de un sistema de coordenadas geográficas, un sistema de coordenadas proyectadas posee longitudes, ángulos y áreas constantes en las dos dimensiones. Un sistema de coordenadas proyectadas siempre está basado en un sistema de coordenadas geográficas basado en una esfera o un esferoide” (ESRI 2023a).

Cuando se trabaja con datos espaciales es importante que todos ellos estén definidos en el mismo SRC, para que sean compatibles entre sí. Por ejemplo, si tengo datos de puntos que representan hospitales en un barrio, digamos el barrio Central, pero el polígono que representa a dicho barrio está en un SRC diferente al de los puntos, la representación de los hospitales en el polígono no se corresponderá con la realidad.

A través de diversos programas es posible cambiar el sistema de referencia de coordenadas, es decir, reproyectar un conjunto de datos vectoriales desde un CRS a otro distinto. Es particularmente útil cambiar la proyección desde un sistema de coordenadas geográficas a un sistema de coordenadas proyectadas cuando se pretende calcular distancias. Esta operación puede ejecutarse de forma muy sencilla en programas como QGIS, o bien en R, pero ello está fuera del interés de este capítulo.

Usando la función plot() que pertenece al paquete graphics, es posible elaborar una primera representación de algunas de las variables de nuestra base. Esto es sólo para darnos cuenta de que ahora tratamos con información espacial, es decir, objetos espaciales (unidades adminsitrativas: alcaldías y municipios) a los que se asocian determinados atributos o variables.

graphics::plot(zmvm_cov_sf)

## Warning: plotting the first 9 out of 57 attributes; use max.plot = 57 to plot
## all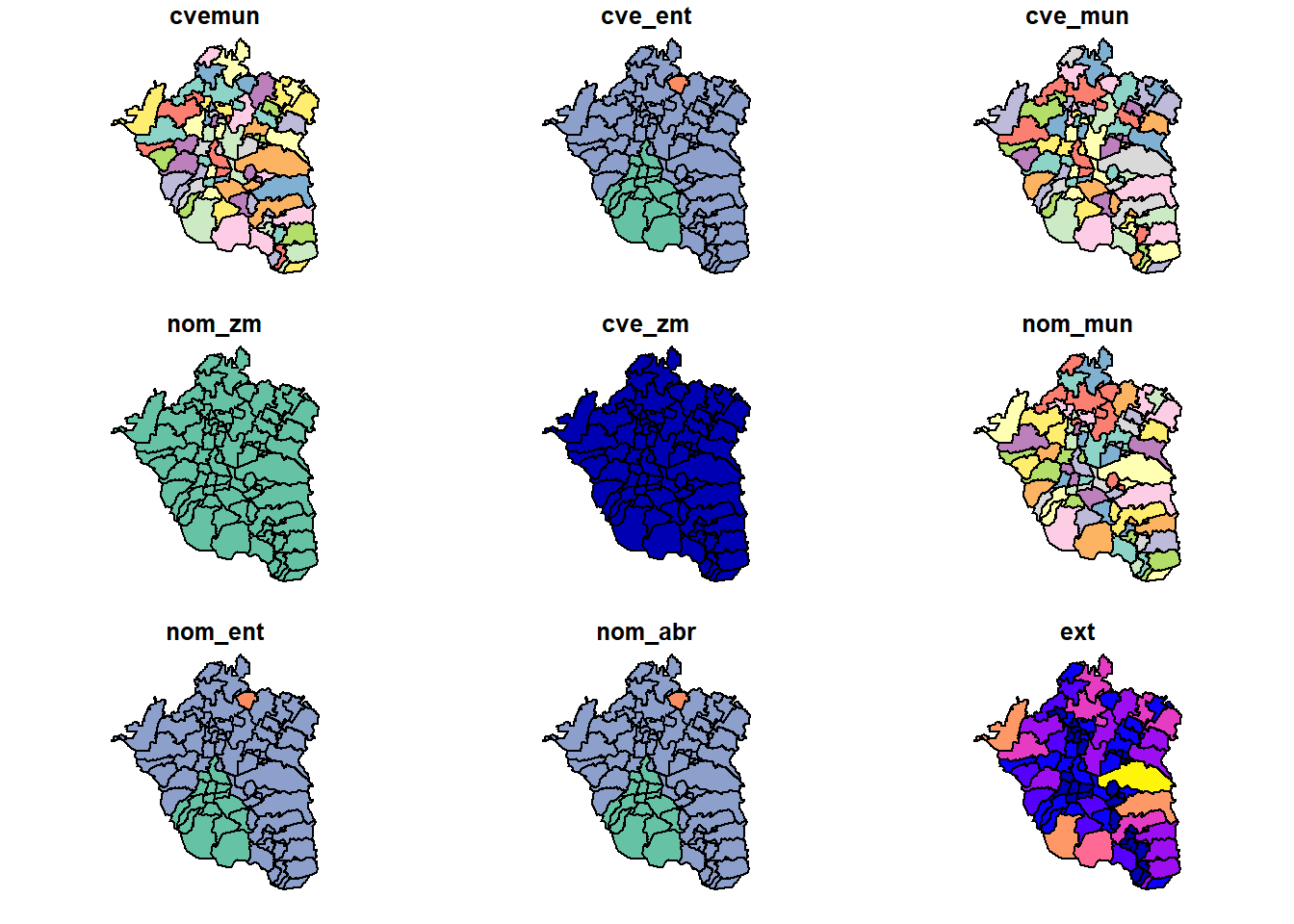

2.4 Mapas coropléticos básicos

Los mapas de coropletas o mapas coropléticos se construyen en R con el paquete tmap. Este tipo de mapas, que pertenece a la categoría más general de los llamadso mapas temáticos, permiten representar la distribución espacial de una variable, es decir, cómo luce la variable representada el espacio geográfico considerado; por ejemplo, el número de casos positivos por COVID19 en alguna región de México. De nueva cuenta, te recomendamos revisar el libro de Víctor Olaya, en la sección El mapa y la comunicación cartográfica, para una exposición más amplia sobre la representación de información espacial a través de mapas.

La lógica de la construcción de mapas con tmap es semejante a la de ggplot2: se usan “enunciados” para completar diferentes elementos del mapa. Así, para construir un mapa completo habrá que indicar, la mayor parte de las veces, tres elementos: i) la geometría de origen (función tm_shape()), ii) los límites internos de las formas utilizadas (función tm_borders()), y iii) la manera en que han de ser rellenados con colores los polígonos según los valores de una variable (función tm_fill()).

Así, la elaboración de nuestro mapa implica un segmento de código con tres elementos:

tmap::tm_shape("capa shp origen de la información")+
  tmap::tm_borders("elementos de edición del borde interno")+
  tmap::tm_fill("elementos de edición del relleno y representación de la variable")

Resulta evidente que el segmento de código anterior arrojará un error si lo ejecutas en tu consola, pues hay que especificar los argumentos del caso, sustituyendo las expresiones entrecomilladas. Por ejemplo, para representar nuestra información usando los tres elementos para la variable pos_hab, número de casos positivos de COVID19 por cada mil habitantes, tenemos:

tmap::tm_shape(shp=zmvm_cov_sf)+
  tmap::tm_borders()+
  tmap::tm_fill("pos_hab")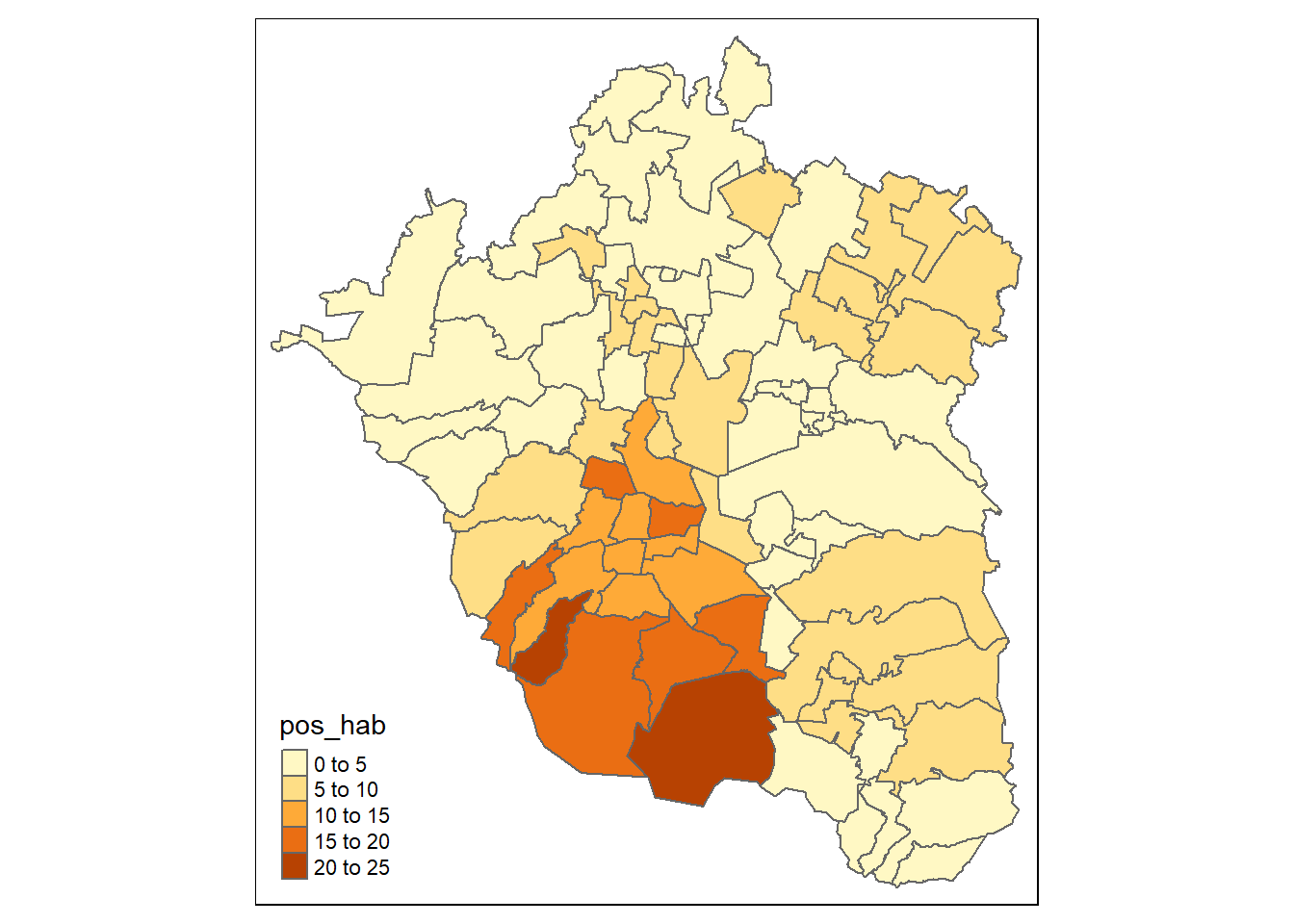

Nota cómo dentro de la función de borde se encuentran operando argumentos por defecto, es decir, que sin indicar ningún argumento específico (como tipo de borde o ancho), arroja un resultado. Sobre dichos argumentos volveremos después.

---

Ejercicio

Prueba eliminando alternativamente una de las funciones de la triada anterior. ¿Qué resultado obtienes con cada combinación?

---

Alternativamente, una manera rápida de suplir las funciones de borde y relleno es sustituirlas con la función tm_polygons()

tmap::tm_shape(zmvm_cov_sf)+
  tmap::tm_polygons(col="pos_hab")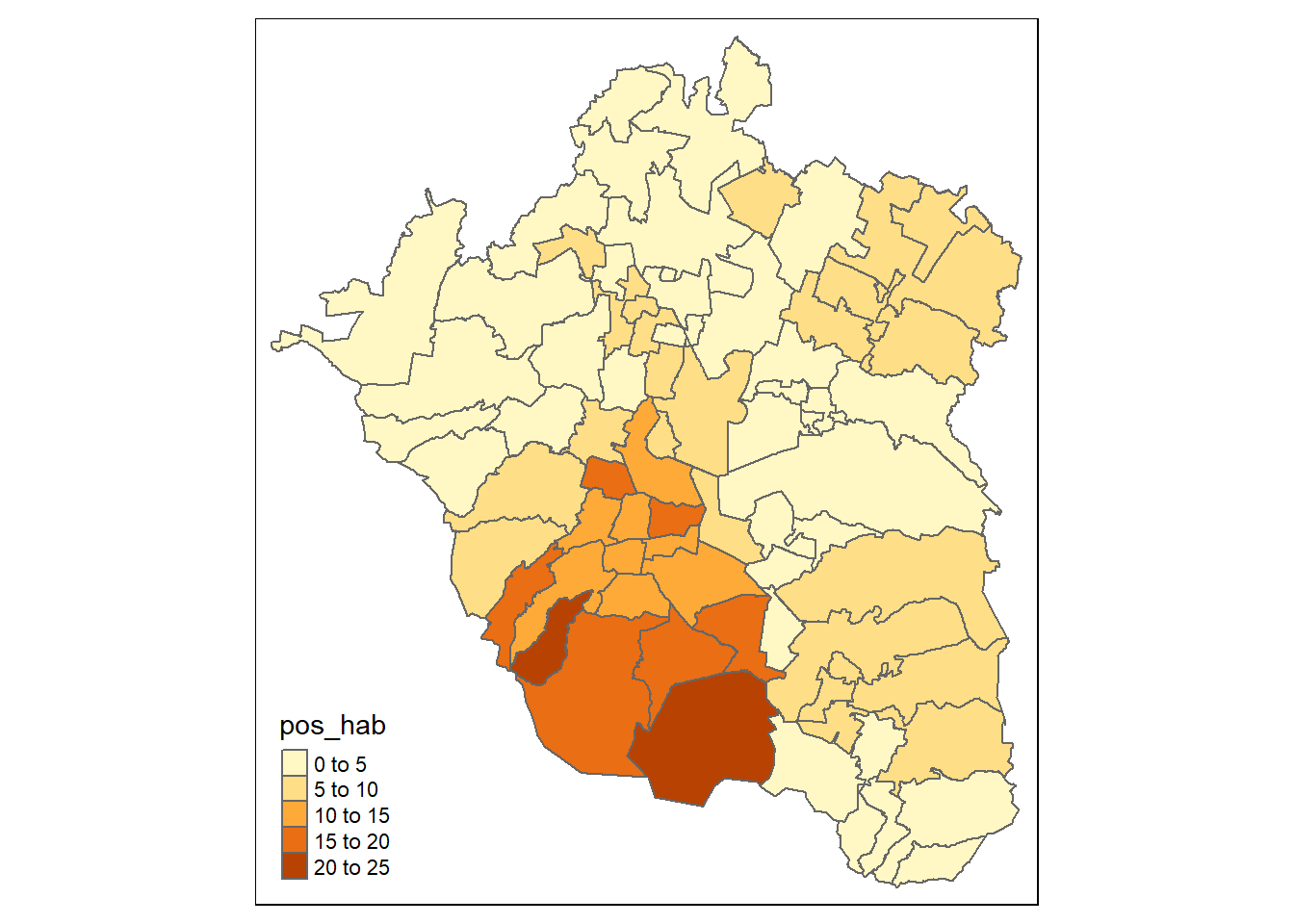

La función tm_polygons() representará la variable indicada en el argumento col=. Además, tanto en esta función como en la de relleno, tm_fill(), el método de clasificación es el método o estilo estético o “bonito” en el que los cortes o categorías se dividen en números enteros siempre que sea posible y los espacia uniformemente (argumento style = "pretty").

Con lo anterior, tienes ya las bases y la lógica para construir mapas coropléticos en R, lo demás no son más que elementos de personalización para cada una de las funciones previas, además de la incorporación de funciones adicionales para elaborar mapas mucho más profesionales.

Te recomendamos consultar, además del libro de Víctor Olaya ya comentado previamente, el espléndido material Geocomputation with R de (Lovelace, Nowosad, and Muenchow 2019), así como el material y todo lo relacionado con el paquete tmap en tmap: Thematic Maps in R (Tennekes 2018).

2.5 Personalización

2.5.1 Argumentos de personalización dentro de la función de relleno

2.5.1.1 Paleta de colores

Nos concentraremos ahora en revisar cómo podemos hacer “mapas a la medida”, es decir, personalizar prácticamente cada parte del mapa, desde la paleta de colores hasta títulos y leyendas. Comencemos revisando las posibilidades de personalización dentro de la función de relleno, tm_fill(). Veremos primero cómo cambiar la paleta de colores de relleno a través del argumento palette=. Por defecto, los colores corresponden a una gama cromática de rojos, pero podemos cambiarla a una de color naranja:

tmap::tm_shape(zmvm_cov_sf)+
  tmap::tm_borders()+
  tmap::tm_fill("pos_hab", palette = "Oranges")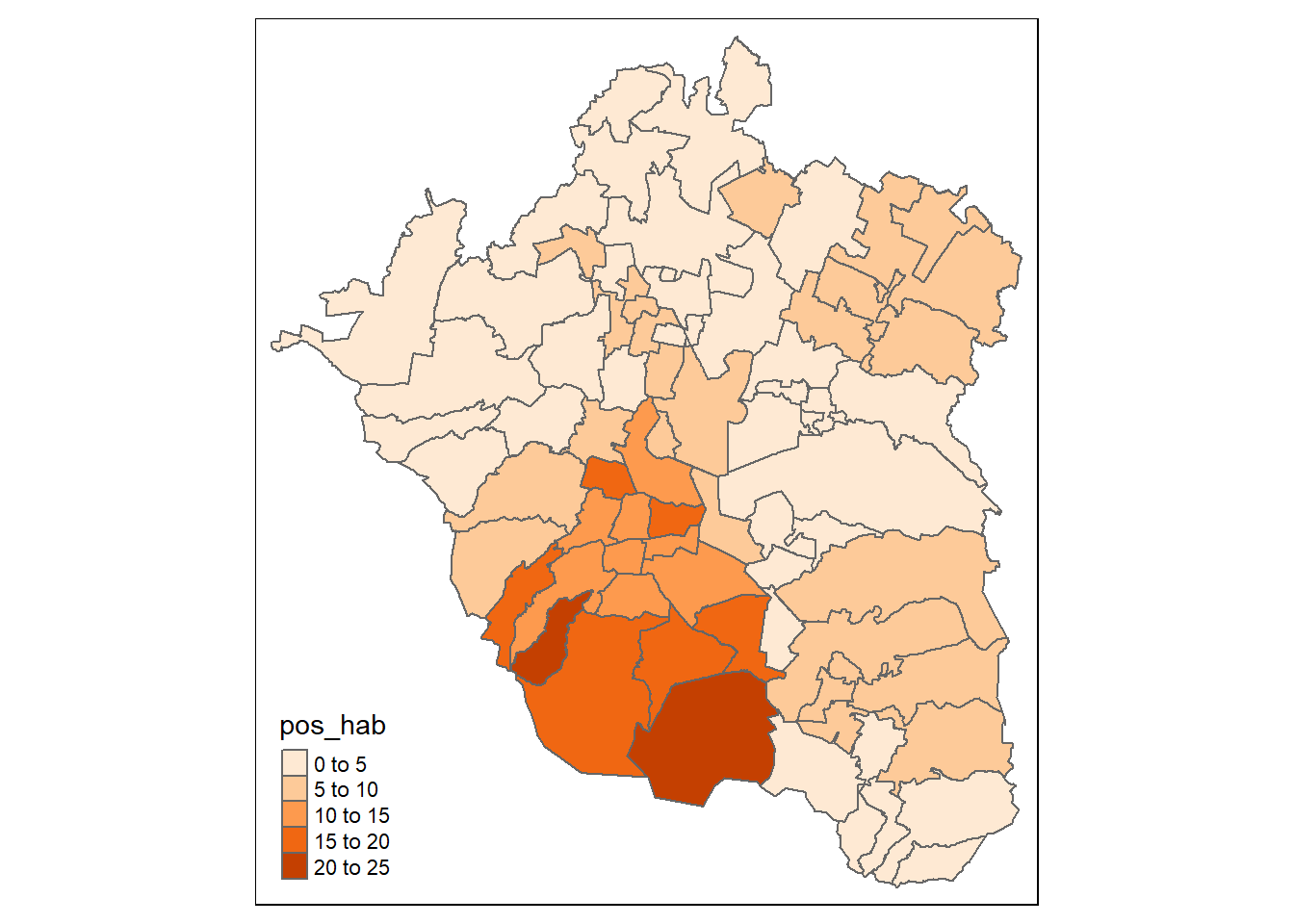

---

Ejercicio

Prueba cambiar el esquema de colores por aquellos que sean de tu gusto, ¿cuáles son los colores admitidos por R dentro del argumento de paleta?

---

Una manera alternativa de cambiar la paleta de colores consiste en fijar un color para la clase inicial y uno para la clase final, como si se tratara de colores ancla. Para ello nos servimos de un vector como valor del argumento palette=:

tmap::tm_shape(zmvm_cov_sf)+
  tmap::tm_borders()+
  tmap::tm_fill("pos_hab", palette = c("blue","red"))

Para tener una paleta divergente insertamos otro color en el centro:

tmap::tm_shape(zmvm_cov_sf)+
  tmap::tm_borders()+
  tmap::tm_fill("pos_hab", palette = c("blue","white", "red"))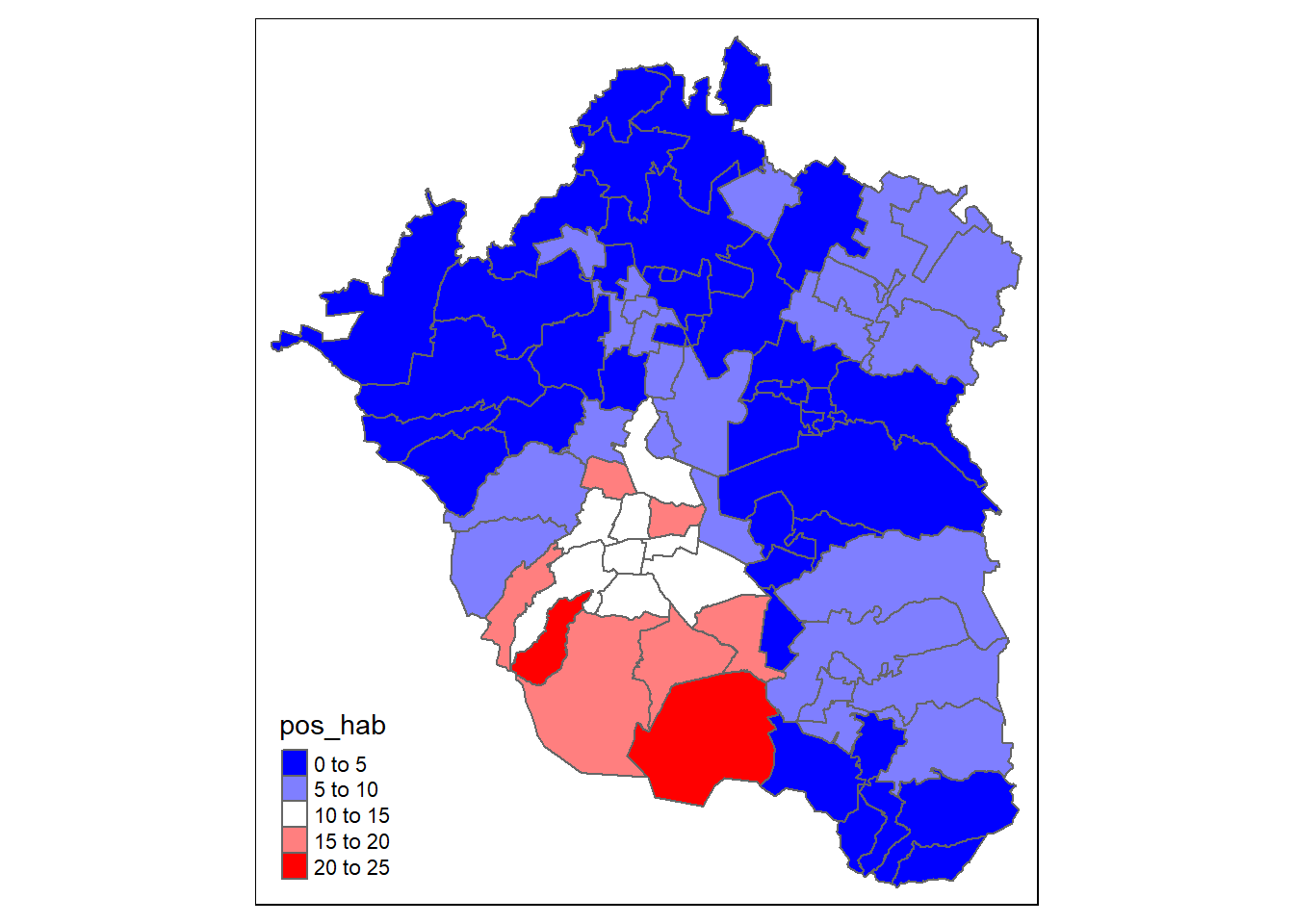

No obstante, la manera más adecuada para la selección de una paleta de colores en términos de comunicación visual es través las propuestas de especialistas, como las de la célebre cartógrafa estadounidense Cynthia Brewer.

El uso de una determinada paleta de colores depende de la idea a transmitir, del tipo de datos a representar, de si el mapa será impreso o digital e incluso de a quién va dirigido. El términos generales, se puede hacer uso de tres tipos de paletas: i) secuenciales, ii) divergentes y iii) cuantitativas. Las primeras son adecuadas para ordenar datos en forma ascendente, lo que permite observar la distribución espacial de la variable y facilita la identificación de patrones de asociación, en tanto, las paletas divergentes están diseñadas para hacer énfasis en valores extremos (muy altos o muy bajos) y facilitan su identificación en el espacio, finalmente, las paletas cuantitativas buscan clasificar variables categóricas, sin algún orden de magnitud definido. Una exposición más detallada de las paletas de colores y sus usos puede ser consultada aquí.

La doctora Brewer diseñó toda una serie de paletas para la representación de información espacial en función del tipo de variable a representar y del número de categorías deseadas para clasificar la información. En R, se cuenta con el paquete RColorBrewer que permite, siguiendo los principios de la doctora Brewer, elegir entre una amplia gama de posibilidades de paletas de colores, ya sea secuenciales, divergentes o cualitativas. Además, el paquete permite crear un esquema de colores personalizado indicando los “colores ancla” y el número de categorías.

Ilustremos cómo nos servimos del paquete RColorBrewer para crear una paleta de seis colores, en una gama cromática del azul al verde. La función brewer.pal() es la indicada para ello:

RColorBrewer::brewer.pal(6,"BuGn")

## [1] "#EDF8FB" "#CCECE6" "#99D8C9" "#66C2A4" "#2CA25F" "#006D2C"

Los códigos hexagesimales resultado de la función anterior poco nos dicen sobre colores, entonces, hay que visualizarlos. Para ello hemos de usar la función display.brewer.pal()

RColorBrewer::display.brewer.pal(6,"BuGn")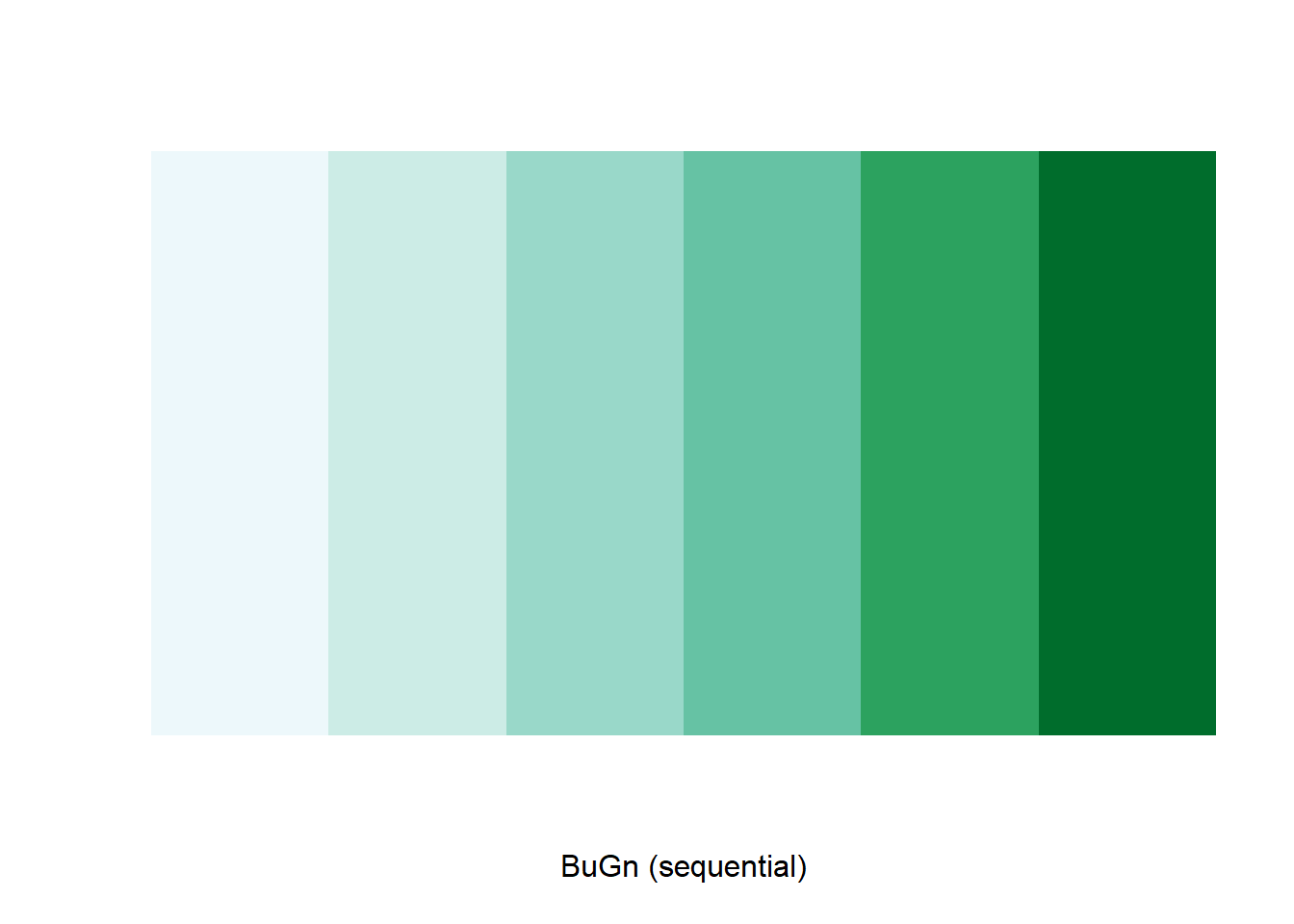

Ahora, ya que tenemos una paleta que luce más estética, podemos aplicarla a nuestro mapa:

tmap::tm_shape(zmvm_cov_sf)+
  tmap::tm_borders()+
  tmap::tm_fill("pos_hab", palette = "BuGn" )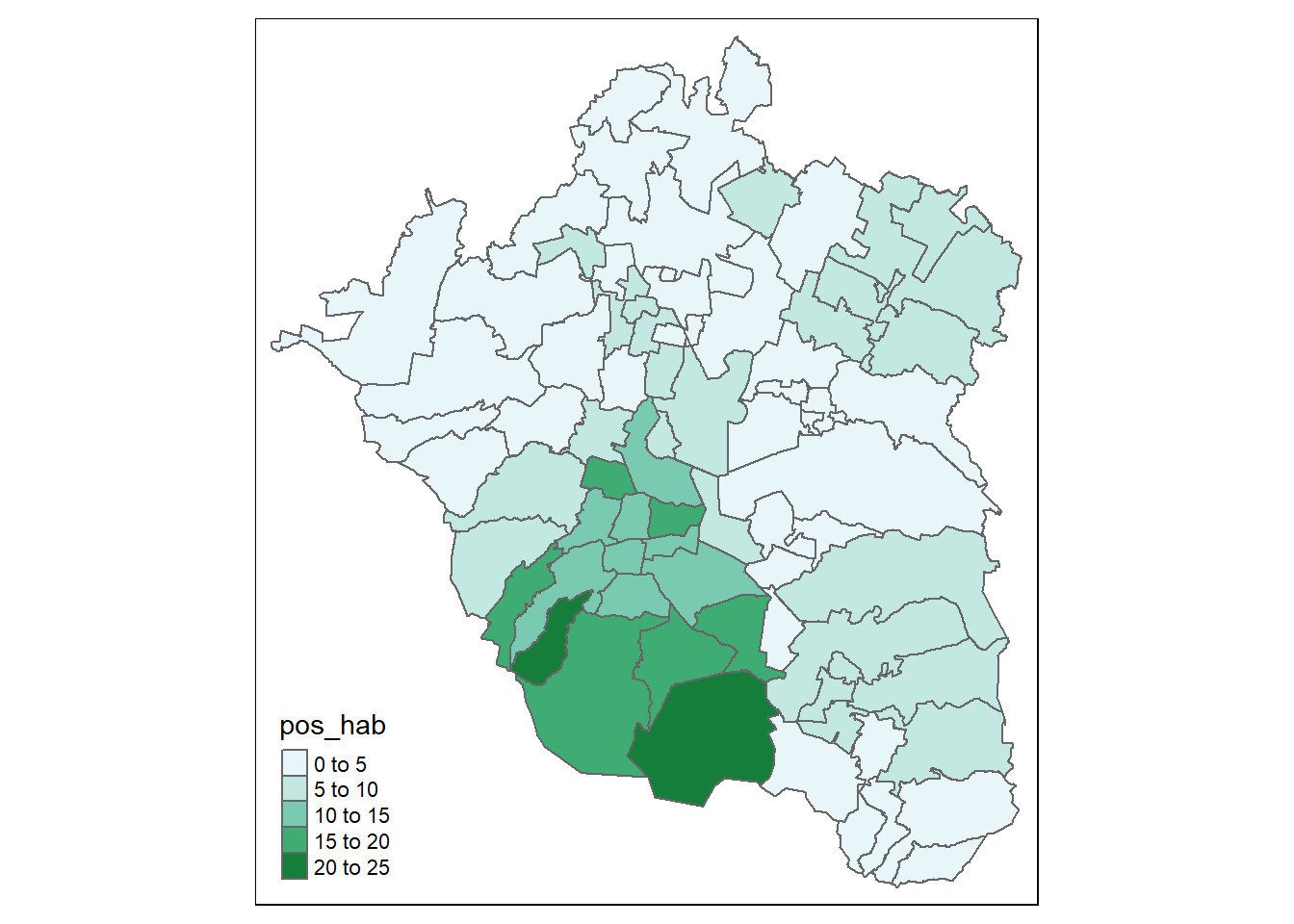

---

Ejercicio

1. Solicita ayuda del paquete RColorBrewer para ver los diferentes tipos de paletas (con las que se cuenta (secuenciales, divergentes y cualitativas) e intenta hacer algunos mapas con dichas paletas.

2. Ejecuta el siguiente segmento de código para explorar una aplicación con shiny, otro paquete más de R, que te permitirá ver todas las posibilidades de paletas creadas por la doctora Brewer.

install.packages("shiny","shinyjs")#Instala Shiny y sus dependencias
tmaptools::palette_explorer() #Lanza la aplicación de Shiny para mostrar las paletas Brewer
#El modo estatico del libro no permite que se pueda correr este codigo, no obstante, con R en ejecución no existe ningún problema

---

2.5.1.2 Leyenda

Para modificar el título de la leyenda, el argumento del caso es justamente title=, dentro de la función tm_fill(), a través de una cadena de texto. Por ejemplo:

tmap::tm_shape(zmvm_cov_sf)+
  tmap::tm_borders()+
  tmap::tm_fill("pos_hab", title = "Casos positivos COVID19")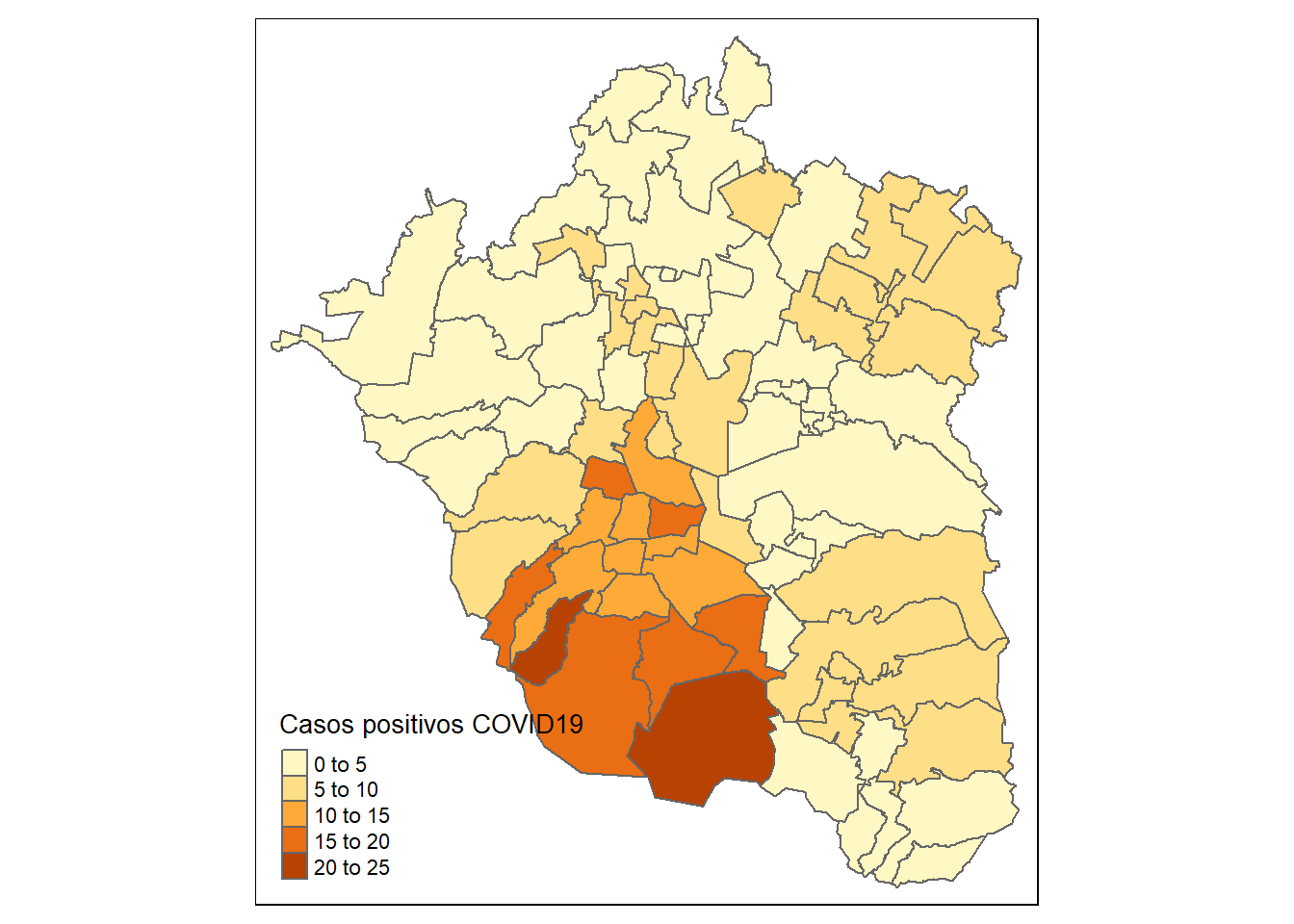

Podemos también agregar elementos informativos adicionales a nuestro mapa, como un histograma, a través del argumento lógico legend.hist=:

tmap::tm_shape(zmvm_cov_sf)+
  tmap::tm_borders()+
  tmap::tm_fill("pos_hab", title = "Casos positivos COVID19",legend.hist = TRUE)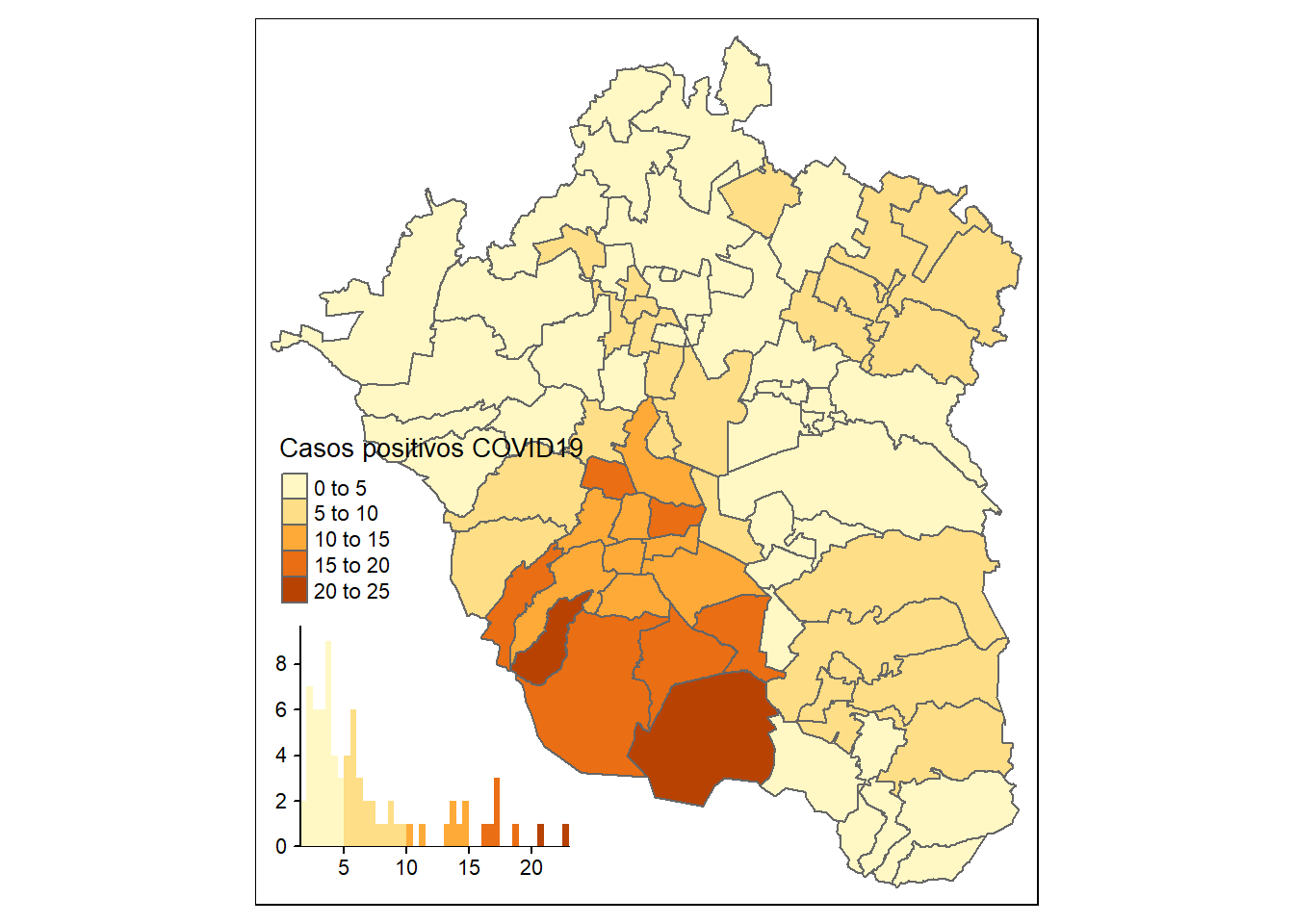

Como habrás notado, hay infinidad de elementos que es posible modificar. Particularmente para el caso de la leyenda del mapa, su formato está gobernado por el argumento legend.format= en el que es posible especificar desde las etiquetas, el formato de los números, sufijos o prefijos de las categorías, entre otros tantos elementos. Solicita ayuda sobre la función tm_fill() y observa los argumentos que la integran. Cerramos esta sección mencionando únicamente cómo cambiarla leyenda de nuestro mapa para que las etiquetas de ésta queden en castellano (para que diga “0 a 5” en vez de “0 to 5”). Esto lo hacemos añadiendo el argumento citado, legend.format=, en el que especificamos, mediante una lista, cómo debe lucir el texto que separa los valores de cada una de las categorías de nuestra leyenda legend.format = list(text.separator="a"):

tmap::tm_shape(zmvm_cov_sf)+
  tmap::tm_borders()+
  tmap::tm_fill("pos_hab",
                palette = "BuGn",
                legend.format = list(text.separator="a") )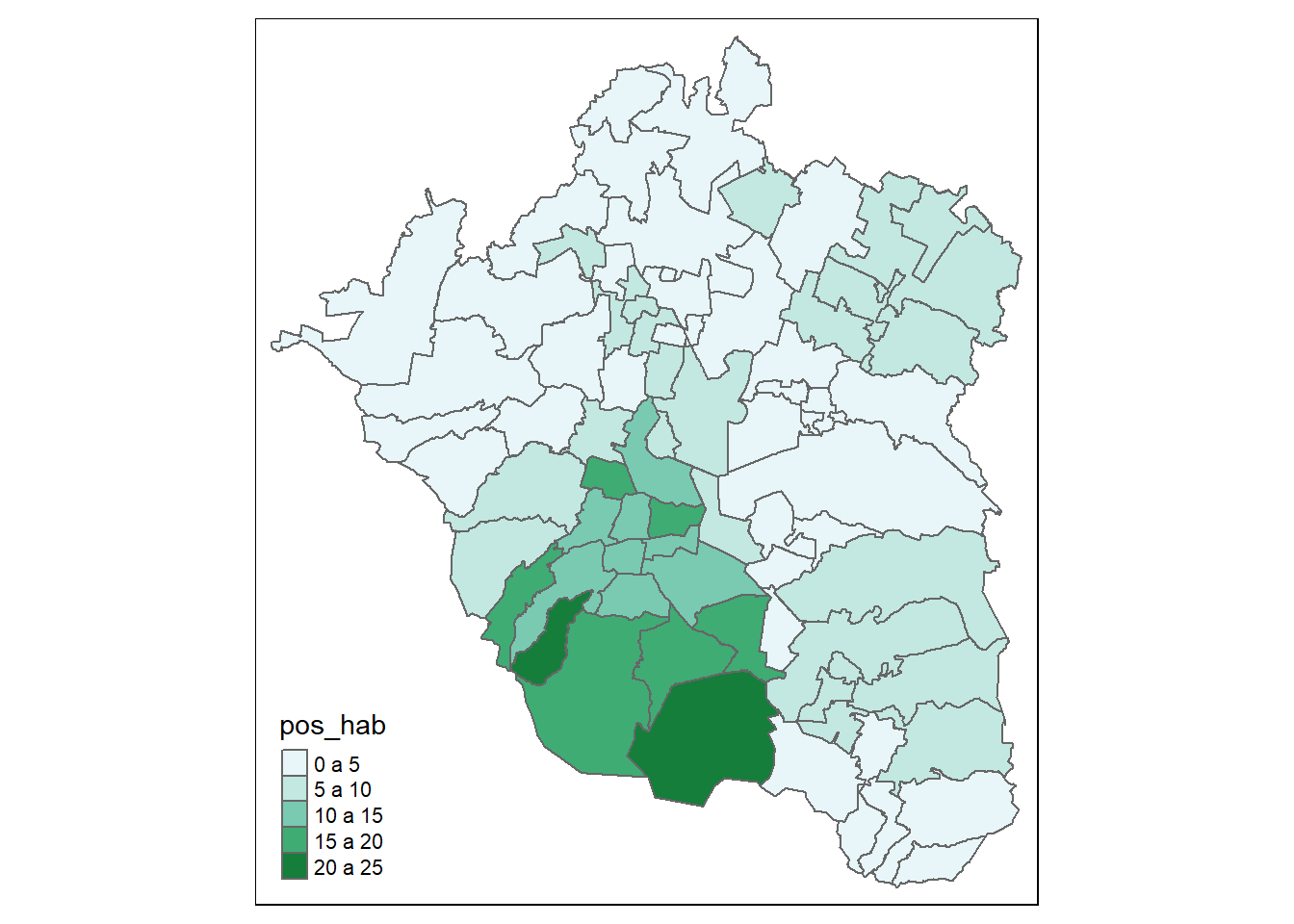

2.5.1.3 Métodos de clasificación en los mápas

Quizá el elemento de personalización más importante en la edición de mapas tiene que ver con el método de clasificación de la variable que busca ser representada. Todas las alternativas de cómo deben construirse las categorías resultado de la clasificación deben ser especificadas dentro de la función tm_fill().

Hay diferentes métodos de clasificación y, por tanto, diferentes tipos de mapas según el método de clasificación. Podemos organizar dichos tipos de mapas de coropletas en tres grandes familias, tal como se muestra en el cuadro 2.1:

Cuadro 2.1. Formas de clasificación de familias de mapas

Familia	Objetivo	Tipos de mapa
Clasificación común	Conocer la distribución espacial del atributo de interés a través de diversos métodos de clasificación.	- Cuantiles - Intervalos iguales - Cortes naturales - Jenks - Cortes estéticos
Clasificación especial	Conocer si la variable presenta algún valor atípico y representar su ubicación.	- Percentiles - Desviación estándar
Clasificación por categorías preexistentes	Conocer la distribución espacial de una categoría predefinida.	- Caja - Valores únicos

Todos estos tipos de mapas pueden ser fácilmente invocados en un programa como GeoDa o QGIS, sin embargo, hasta donde sabemos, en R no todos están disponibles y a veces la construcción de alguno de ellos exige algunos fundamentos de programación. A pesar de ello, R ofrece bastantes alternativas sencillas para construir mapas de clasificación común.

---

Ejercicio

Ve a la ayuda de la función tm_fill(), identifica el argumento style=, sigue la documentación sugerida y responde:

1. ¿Cuántos métodos de clasificación ofrece R?
   

2. ¿En qué consiste el método de clasificación de k-medias?
   

3. ¿En el trabajo de quiénes está basado el método de clasificación fisher?.

---

Los mapas que es posible construir en R sin mayores complicaciones se muestran en el cuadro 2.2, así como los valores que debes indicar en el argumento del caso:

Cuadro 2.2. Tipos de mapas

Tipo de mapa	Argumento tmap::tm_fill(style=)
Cuantiles	style=quantile
Intervalos iguales	style=equal
Cortes naturales o Jenks	style=jenks
Cortes estéticos	style=pretty

Como se dijo, los mapas de clasificación común quedarán indicados en los argumentos de la función tm_fill(). Para construir un mapa de 5 cuantiles (quintiles), que es la opción por defecto para el número de categorías:

tmap::tm_shape(zmvm_cov_sf) +
  tmap::tm_borders()+
  tmap::tm_fill("pos_hab", style = "quantile", title = "Casos positivos")+
  tmap::tm_layout(title = "Mapa de cuantiles", title.position = c("center", "bottom"))#Más adelante se explica esta función

Si deseas cambiar el número de categorías, por ejemplo a cuatro, deberás indicar explícitamente su número en el argumento n=:

tmap::tm_shape(zmvm_cov_sf) +
  tmap:: tm_borders()+
  tmap::tm_fill("pos_hab", n= 4, style = "quantile", title = "Casos positivos")+
  tmap::tm_layout(title = "Mapa de cuantiles", title.position = c("center", "bottom"))#Más adelante se explica esta función

---

Ejercicios

Construye:

1. Un mapa de Jenks con 6 categorías.

2. Un mapa de intervalos iguales con cuatro categorías.

3. Un mapa a partir de la clasificación por clusters jerárquicos.

---

2.5.2 Argumentos de personalización del borde

Se dijo antes que a pesar de no haber especificado argumento alguno en la función de borde, en ésta operan argumentos por defecto. Es momento de modificar dichos argumentos. Las opciones de borde se especifican dentro de tm_border() donde es posible modificar el color (col=), grosor (lwd=) y tipo de borde (lty=):

tmap::tm_shape(zmvm_cov_sf)+
  tmap::tm_fill("pos_hab")+
  tmap::tm_borders(col="black",lwd=2, lty = 3)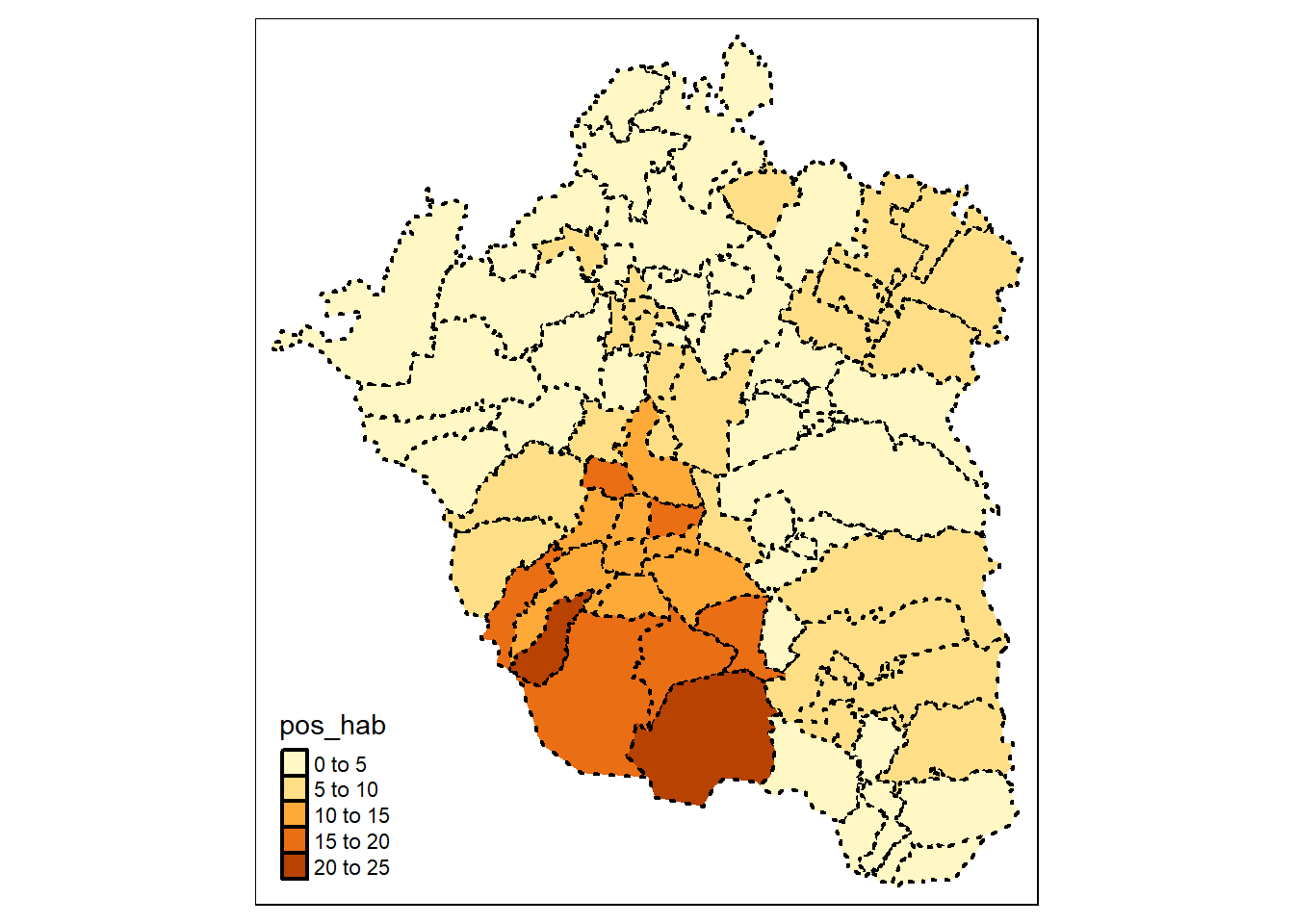

---

Ejercicio

Solicita ayuda de la función tm_fill() y explora qué otras opciones de borde existen. Haz algunos mapas para la variable def_hab cambiando el tipo de borde.

---

2.6 Función para elementos de diseño de salida, tm_layout()

Con la combinación de las funciones previamente descritas se puede generar un mapa básico, además, dentro de ellas es posible personalizar múltiples elementos. No obstante, un diseño más adecuado y profesional es logrado a través de la función tm_layout(), que abarca, entre otras cosas, la posición de la leyenda, el título principal del mapa y tamaños de fuente. Veamos cómo opera.

Para cambiar la posición de la leyenda, los argumentos deben colocarse dentro de la función, tm_layout(), a través de un vector que indique tanto la orientación vertical como la horizontal de la leyenda. Para la orientación horizontal: "left","right" o "center" y para la vertical: "top", "center" o "bottom", tal que:

tmap::tm_shape(zmvm_cov_sf)+
  tmap::tm_fill("pos_hab")+
  tmap::tm_borders()+
  tmap::tm_layout(legend.position = c("right", "bottom"))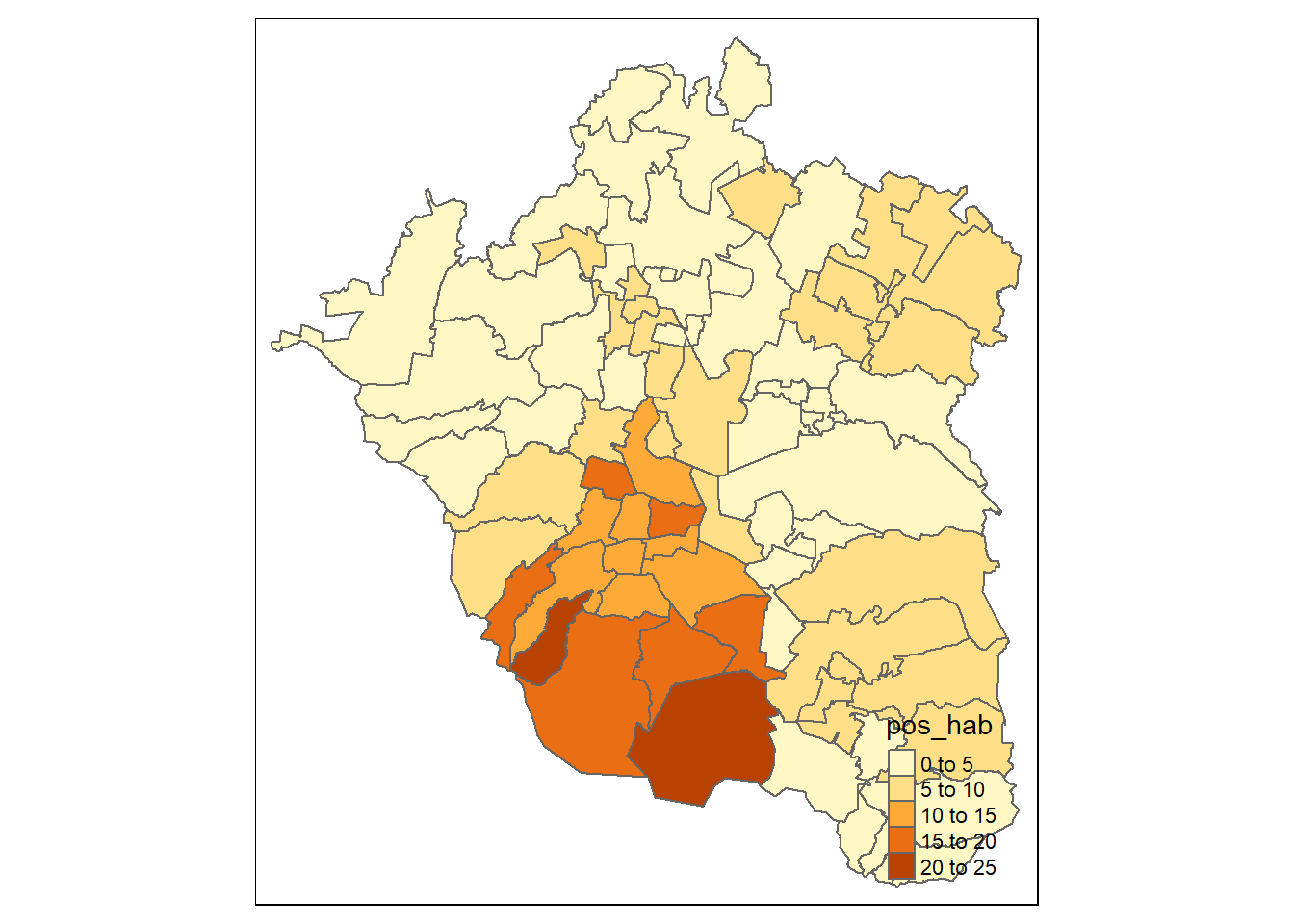

Para posicionar la leyenda fuera del mapa, dentro de la función tm_layout() usa el argumento lógico legend.outside y si deseas especificar la posición, el argumento será legend.outside.position que tomará los valores tipo texto de "top", "bottom", "right" o "left". Por ejemplo:

tmap::tm_shape(zmvm_cov_sf)+
  tmap::tm_fill("pos_hab")+
  tmap::tm_borders()+
  tmap::tm_layout(legend.outside = TRUE,legend.outside.position = "left")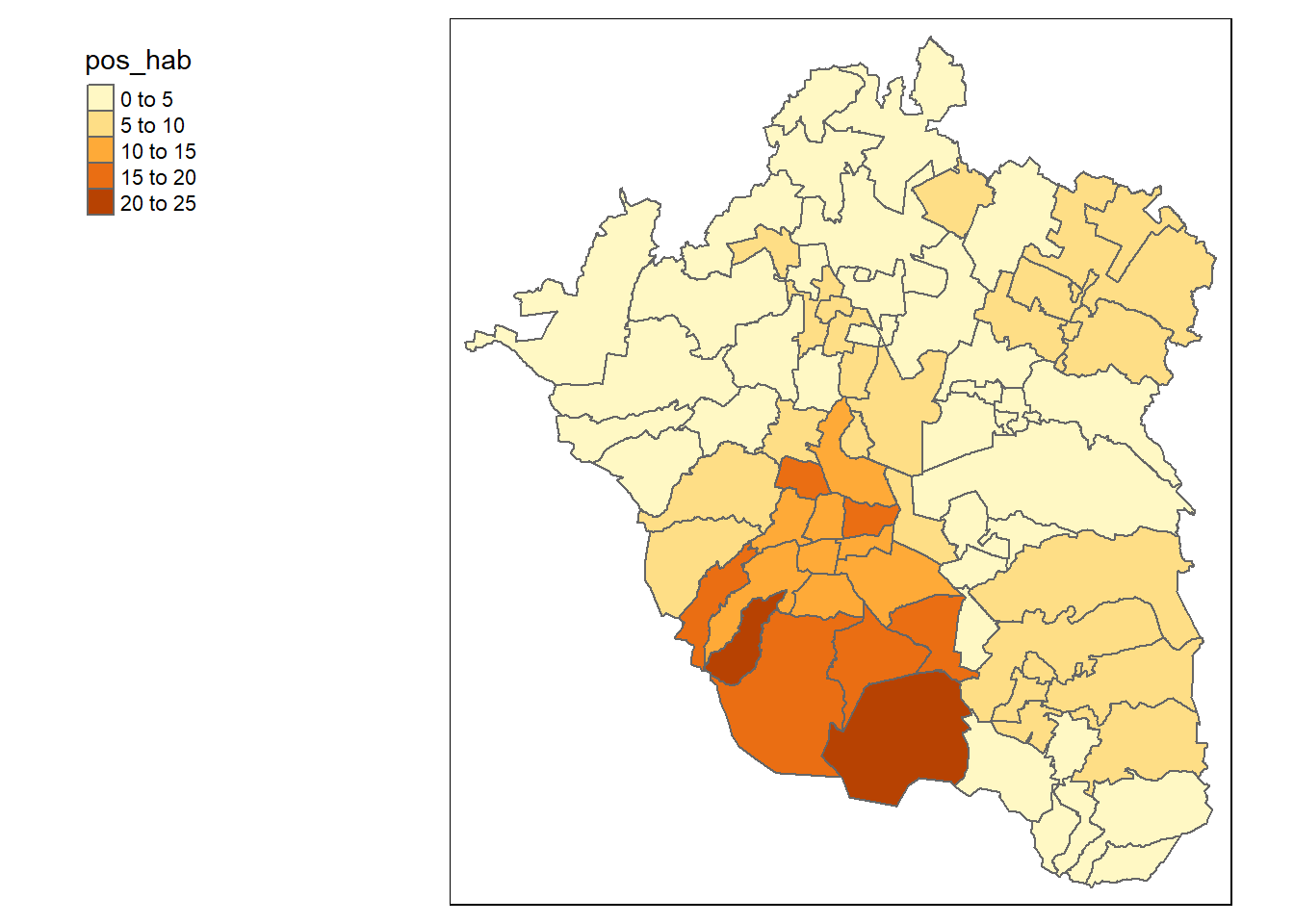

Para personalizar el título dentro del mapa, en la función tm_layout() hay que agregar el argumento title= y para la posición: title.position=:

tmap::tm_shape(zmvm_cov_sf)+
  tmap::tm_borders()+
  tmap::tm_fill("pos_hab", title = "Casos positivos COVID19")+
  tmap::tm_layout(title = "Casos positivos COVID19 por cada mil habitales", title.position = c("center","top"))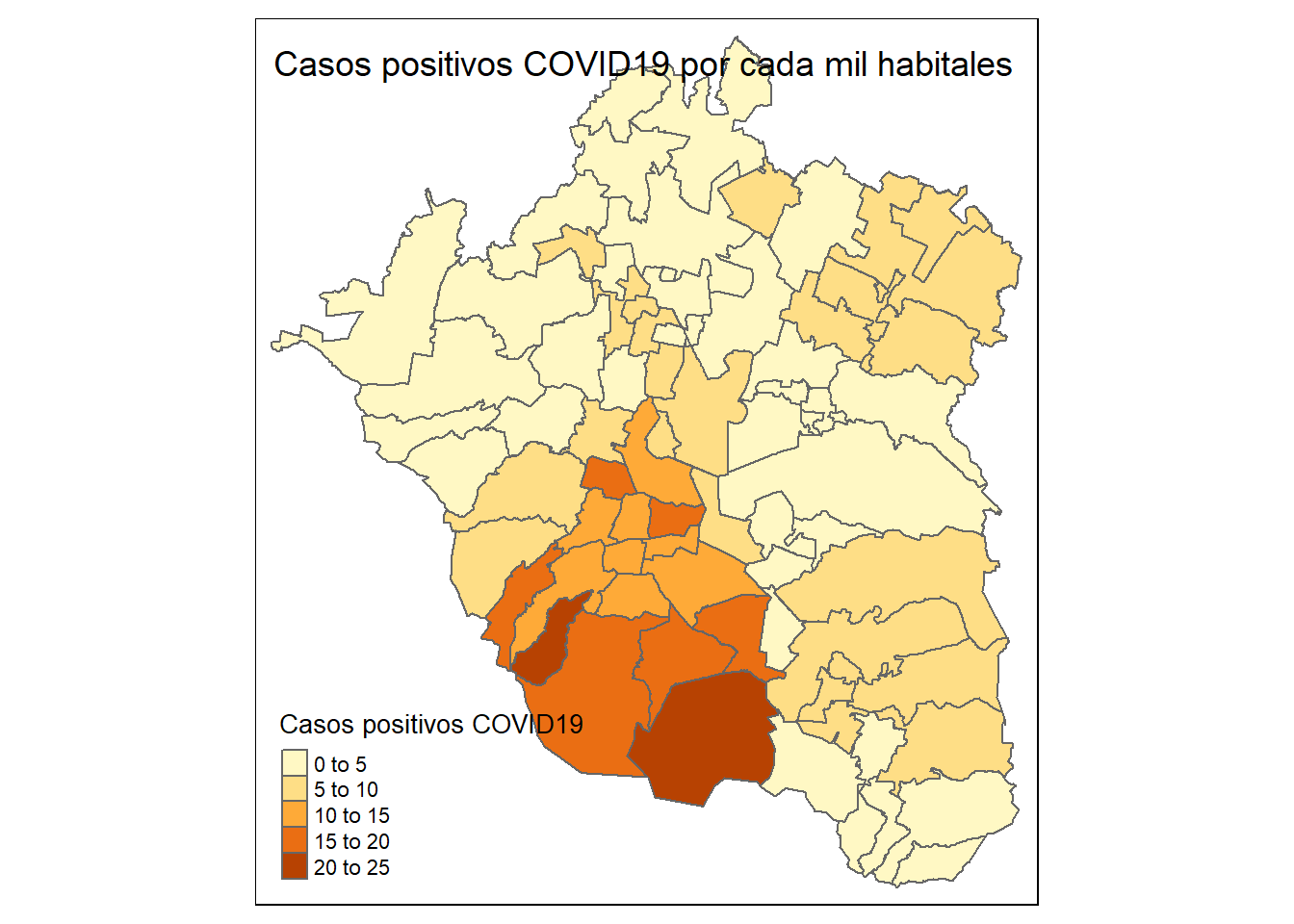

O bien, si queremos el título afuera del mapa, con un tamaño de fuente diferente y centrado:

tmap::tm_shape(zmvm_cov_sf)+
 tmap:: tm_borders()+
  tmap::tm_fill("pos_hab", title = "Ingreso 2010")+
  tmap::tm_layout(main.title = "Casos positivos COVID19 por cada mil habitantes", main.title.position = "center", title.size = 1.3)

2.7 Mapa base interactivo

En R es posible añadir a nuestros mapas temáticos un mapa base para dar contexto a nuestra representación. Para ello, es necesario activar una suerte de “modo interactivo”, para ser más exactos, lo que activamos es el modo de visualización para poder desplazarnos sobre los mapas. Para cambiar al modo de visualización:

tmap::tmap_mode("view")

## tmap mode set to interactive viewing

La función que permite agregar mapas base es tm_basemap().

---

Ejercicio

¿Cuántos tipos de mapas base es posible usar en R? Revisa la ayuda de la función y familiarízate con sus argumentos.

---

De los argumentos para el mapa base, dos son los básicos: el servidor de donde tomaremos el mapa (consejo: ya dentro de los argumentos de la función, escribe providers$ y observarás todas las opciones disponibles) y transparencia (argumento alpha=) que toma valores de 0 a 1; el argumento alpha= altera tanto la transparencia del mapa base cuando es usado dentro de la función tm_basemap(), como la transparencia de los colores usados para representar la información si se usa dentro de la función tm_fill(). Ejecuta el siguiente segmento de código y navega sobre el mapa representado:

tmap::tm_shape(zmvm_cov_sf)+
  tmap::tm_borders()+
  tmap::tm_fill("pos_hab", alpha=0.7)+
  tmap::tm_basemap(providers$OpenStreetMap,alpha = 0.5)

Una vez que has terminado de navegar y trabajar con mapas base es necesario desactivar el modo de visualización y regresar al modo estático:

tmap::tmap_mode("plot")

## tmap mode set to plotting

2.8 Cartograma

Un cartograma es un tipo de mapa que deforma la geometría de las áreas de interés en figuras cuyo tamaño depende de la magnitud de la variable representada. Para elaborar un cartograma con circulos, debemos primero generar la geometría deformada por la variable para luego rellenarla. Para tal efecto, usamos la función cartogram_dorling() que nos permitirá generar un nuevo objeto que contiene las geometrías deformadas. Luego, usaremos dicha geometría como argumento de tm_shape(). Primero creamos la nueva geometría circular:

cartograma_circulos <- cartogram::cartogram_dorling(zmvm_cov_sf,"pos_hab")
class(cartograma_circulos)

## [1] "sf"         "data.frame"

Hay que tener en cuenta que la función sólo admite variables no negativas. Ahora bien, este objeto recién creado será usado tal como lo hemos hecho antes:

tmap::tm_shape(cartograma_circulos) +
  tmap::tm_borders()+
  tmap:: tm_fill("pos_hab")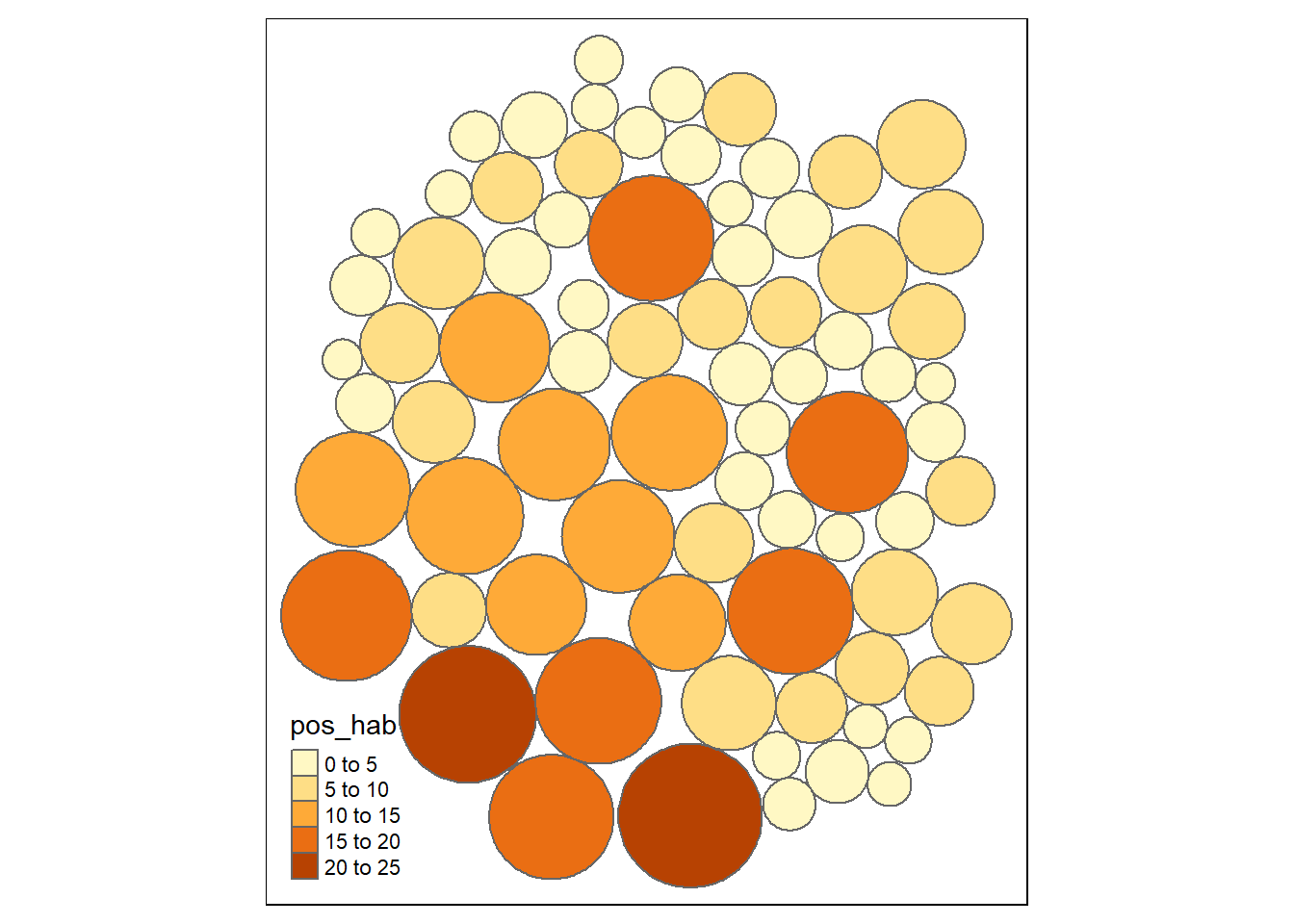

Otro tipo de cartograma, más estético, es aquel que garantiza la contigüidad entre las unidades espaciales después de su deformación. Se procede de forma semejante a lo hecho antes, sólo que ahora usamos la función cartogram_cont():

cartograma_cont <- cartogram_cont(zmvm_cov_sf,"pos_hab")

Ahora, usamos esta información para construir nuestro cartograma:

tmap::tm_shape(cartograma_cont) +
  tmap::tm_fill("pos_hab") +
  tmap:: tm_borders()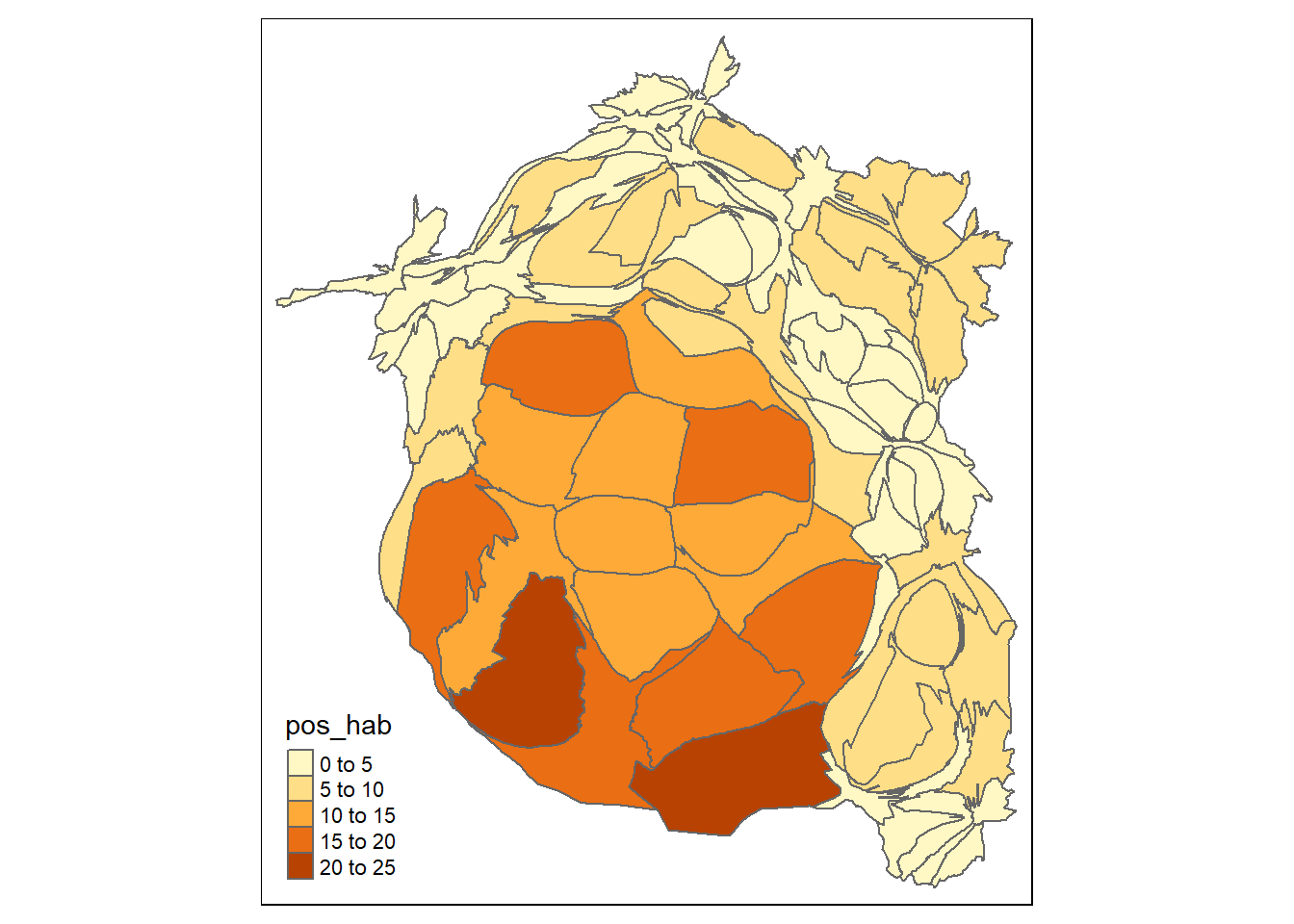

2.9 Centroides o coordenadas geométricas (punto medio)

En el blog de mappingGIS encontramos la siguiente definición de punto medio:

Toda geometría vectorial (punto, línea o polígono) contiene un punto central denominado centroide.

Calcular el centroide de una geometría suele ser una tarea habitual cuando se trabaja con información espacial, por ejemplo, para contar con un punto de referencia a partir del cual contar distancias lineales entre polígonos para definir vecindades, como se verá en el capítulo siguiente. Para crear una nueva capa que contenga los centroides de nuestra geometría usamos en R la función st_centroid(). La función generará una nueva serie de archivos SHP que contendrán el conjunto de variables de la base de datos y los centroides:

zmvm_cntrds <- st_centroid(zmvm_cov_sf)
summary(zmvm_cntrds)

##     cvemun            cve_ent            cve_mun             nom_zm         
##  Length:76          Length:76          Length:76          Length:76         
##  Class :character   Class :character   Class :character   Class :character  
##  Mode  :character   Mode  :character   Mode  :character   Mode  :character  
##                                                                             
##                                                                             
##                                                                             
##      cve_zm       nom_mun            nom_ent            nom_abr         
##  Min.   :9.01   Length:76          Length:76          Length:76         
##  1st Qu.:9.01   Class :character   Class :character   Class :character  
##  Median :9.01   Mode  :character   Mode  :character   Mode  :character  
##  Mean   :9.01                                                           
##  3rd Qu.:9.01                                                           
##  Max.   :9.01                                                           
##       ext             pob20            pob20_h          pob20_m      
##  Min.   :  3.17   Min.   :   4862   Min.   :  2338   Min.   :  2524  
##  1st Qu.: 37.52   1st Qu.:  31900   1st Qu.: 15621   1st Qu.: 16302  
##  Median : 76.22   Median : 160445   Median : 78574   Median : 81871  
##  Mean   :103.51   Mean   : 286902   Mean   :138458   Mean   :148443  
##  3rd Qu.:157.01   3rd Qu.: 432692   3rd Qu.:206156   3rd Qu.:226858  
##  Max.   :434.26   Max.   :1835486   Max.   :887651   Max.   :947835  
##    positivos         defuncione        pos_mil         lag_poshab    
##  Min.   :   18.0   Min.   :   0.0   Min.   : 1.720   Min.   : 2.382  
##  1st Qu.:  131.5   1st Qu.:  13.5   1st Qu.: 3.337   1st Qu.: 3.977  
##  Median :  767.0   Median :  86.0   Median : 5.117   Median : 5.275  
##  Mean   : 2614.0   Mean   : 269.7   Mean   : 6.964   Mean   : 6.733  
##  3rd Qu.: 3617.2   3rd Qu.: 387.0   3rd Qu.: 8.636   3rd Qu.: 8.229  
##  Max.   :18767.0   Max.   :2078.0   Max.   :22.700   Max.   :16.443  
##     pos_hab          def_hab             ss           ppob_sines      
##  Min.   : 1.720   Min.   :0.0000   Min.   :0.5480   Min.   :0.004937  
##  1st Qu.: 3.337   1st Qu.:0.4222   1st Qu.:0.6415   1st Qu.:0.019428  
##  Median : 5.117   Median :0.6528   Median :0.6763   Median :0.023845  
##  Mean   : 6.964   Mean   :0.6735   Mean   :0.6793   Mean   :0.026127  
##  3rd Qu.: 8.636   3rd Qu.:0.8791   3rd Qu.:0.7266   3rd Qu.:0.031717  
##  Max.   :22.700   Max.   :1.6497   Max.   :0.7980   Max.   :0.064699  
##    ppob_basi        ppob_media        ppob_sup           ocviv      
##  Min.   :0.1410   Min.   :0.1645   Min.   :0.07101   Min.   :2.460  
##  1st Qu.:0.4481   1st Qu.:0.2466   1st Qu.:0.13614   1st Qu.:3.530  
##  Median :0.5295   Median :0.2644   Median :0.17064   Median :3.745  
##  Mean   :0.5041   Mean   :0.2624   Mean   :0.20549   Mean   :3.690  
##  3rd Qu.:0.5718   3rd Qu.:0.2831   3rd Qu.:0.25936   3rd Qu.:3.900  
##  Max.   :0.6842   Max.   :0.3235   Max.   :0.67480   Max.   :4.520  
##       occu          pintegra4_       pintegra6_        pintegra8_     
##  Min.   :0.5600   Min.   :0.3657   Min.   :0.06644   Min.   :0.01745  
##  1st Qu.:0.8600   1st Qu.:0.6772   1st Qu.:0.22736   1st Qu.:0.07521  
##  Median :0.9900   Median :0.7161   Median :0.26250   Median :0.08992  
##  Mean   :0.9692   Mean   :0.7013   Mean   :0.26006   Mean   :0.09188  
##  3rd Qu.:1.0625   3rd Qu.:0.7474   3rd Qu.:0.29090   3rd Qu.:0.10844  
##  Max.   :1.2900   Max.   :0.8261   Max.   :0.42810   Max.   :0.20046  
##    ppob_5_o_m       ppob_3_o_m         ppob_1          ppob_1dorm     
##  Min.   :0.6825   Min.   :0.1680   Min.   :0.00611   Min.   :0.08567  
##  1st Qu.:0.7781   1st Qu.:0.3425   1st Qu.:0.03234   1st Qu.:0.20592  
##  Median :0.8183   Median :0.3925   Median :0.04198   Median :0.22763  
##  Mean   :0.8133   Mean   :0.3934   Mean   :0.04413   Mean   :0.23367  
##  3rd Qu.:0.8569   3rd Qu.:0.4406   3rd Qu.:0.05341   3rd Qu.:0.26855  
##  Max.   :0.9150   Max.   :0.5947   Max.   :0.09461   Max.   :0.38234  
##    ppob_2dorm       ppob_3dorm       pviv_ocu5_       pviv_ocu7_      
##  Min.   :0.4875   Min.   :0.7781   Min.   :0.0654   Min.   :0.009724  
##  1st Qu.:0.5883   1st Qu.:0.8581   1st Qu.:0.2434   1st Qu.:0.056245  
##  Median :0.6237   Median :0.8848   Median :0.2835   Median :0.069583  
##  Mean   :0.6307   Mean   :0.8808   Mean   :0.2799   Mean   :0.069614  
##  3rd Qu.:0.6757   3rd Qu.:0.9042   3rd Qu.:0.3209   3rd Qu.:0.082869  
##  Max.   :0.8006   Max.   :0.9484   Max.   :0.4420   Max.   :0.155107  
##    pviv_ocu9_           analf            sbasc             vhac      
##  Min.   :0.002354   Min.   :0.3534   Min.   : 5.535   Min.   : 3.95  
##  1st Qu.:0.015350   1st Qu.:1.6505   1st Qu.:19.915   1st Qu.:16.40  
##  Median :0.020738   Median :1.9798   Median :22.973   Median :21.19  
##  Mean   :0.020961   Mean   :2.3555   Mean   :23.160   Mean   :21.01  
##  3rd Qu.:0.025183   3rd Qu.:2.8267   3rd Qu.:27.193   3rd Qu.:25.00  
##  Max.   :0.060174   Max.   :7.4096   Max.   :41.399   Max.   :38.81  
##      po2sm          idh2015             im          gm_2020         
##  Min.   :28.45   Min.   :0.6240   Min.   :53.57   Length:76         
##  1st Qu.:61.27   1st Qu.:0.7288   1st Qu.:57.36   Class :character  
##  Median :67.40   Median :0.7585   Median :58.46   Mode  :character  
##  Mean   :66.38   Mean   :0.7629   Mean   :58.47                     
##  3rd Qu.:72.76   3rd Qu.:0.7945   3rd Qu.:59.65                     
##  Max.   :86.67   Max.   :0.9290   Max.   :62.36                     
##       grad            grad_h           grad_m           poind        
##  Min.   : 8.080   Min.   : 8.140   Min.   : 8.030   Min.   :0.06475  
##  1st Qu.: 9.557   1st Qu.: 9.658   1st Qu.: 9.490   1st Qu.:0.11379  
##  Median :10.025   Median :10.160   Median : 9.945   Median :0.17993  
##  Mean   :10.252   Mean   :10.376   Mean   :10.139   Mean   :0.19532  
##  3rd Qu.:10.840   3rd Qu.:10.967   3rd Qu.:10.730   3rd Qu.:0.26407  
##  Max.   :14.550   Max.   :14.930   Max.   :14.220   Max.   :0.44291  
##      pocom             poss            tmind            tmcom       
##  Min.   :0.1269   Min.   :0.2113   Min.   : 1.636   Min.   : 1.380  
##  1st Qu.:0.3363   1st Qu.:0.3033   1st Qu.: 3.166   1st Qu.: 1.876  
##  Median :0.4358   Median :0.3610   Median : 5.086   Median : 2.139  
##  Mean   :0.4085   Mean   :0.3961   Mean   : 9.086   Mean   : 2.759  
##  3rd Qu.:0.4970   3rd Qu.:0.4176   3rd Qu.: 9.195   3rd Qu.: 3.009  
##  Max.   :0.6867   Max.   :0.7686   Max.   :48.067   Max.   :10.310  
##       tmss            rmind            rmcom             rmss        
##  Min.   : 1.670   Min.   : 10.26   Min.   : 4.083   Min.   :  2.586  
##  1st Qu.: 2.072   1st Qu.: 30.95   1st Qu.:14.085   1st Qu.: 16.312  
##  Median : 2.775   Median : 63.61   Median :21.002   Median : 28.922  
##  Mean   : 5.765   Mean   : 67.19   Mean   :24.502   Mean   : 39.904  
##  3rd Qu.: 4.604   3rd Qu.: 88.88   3rd Qu.:31.630   3rd Qu.: 52.806  
##  Max.   :41.086   Max.   :177.45   Max.   :67.438   Max.   :255.589  
##       den                   geometry 
##  Min.   :  123.2   POINT        :76  
##  1st Qu.:  463.5   epsg:NA      : 0  
##  Median : 1830.4   +proj=lcc ...: 0  
##  Mean   : 4227.5                     
##  3rd Qu.: 6216.9                     
##  Max.   :17519.3

El conjunto de datos recién creado y que contiene los centroides puede ser representado agregando otra “capa” con la función tm_shape(). En el ejemplo, sólo se superponen las dos capas: la de los polígonos originales y la de los centroides:

tm_shape(zmvm_cov_sf) +
  tm_borders() +
  tm_shape(zmvm_cntrds) +
  tm_dots()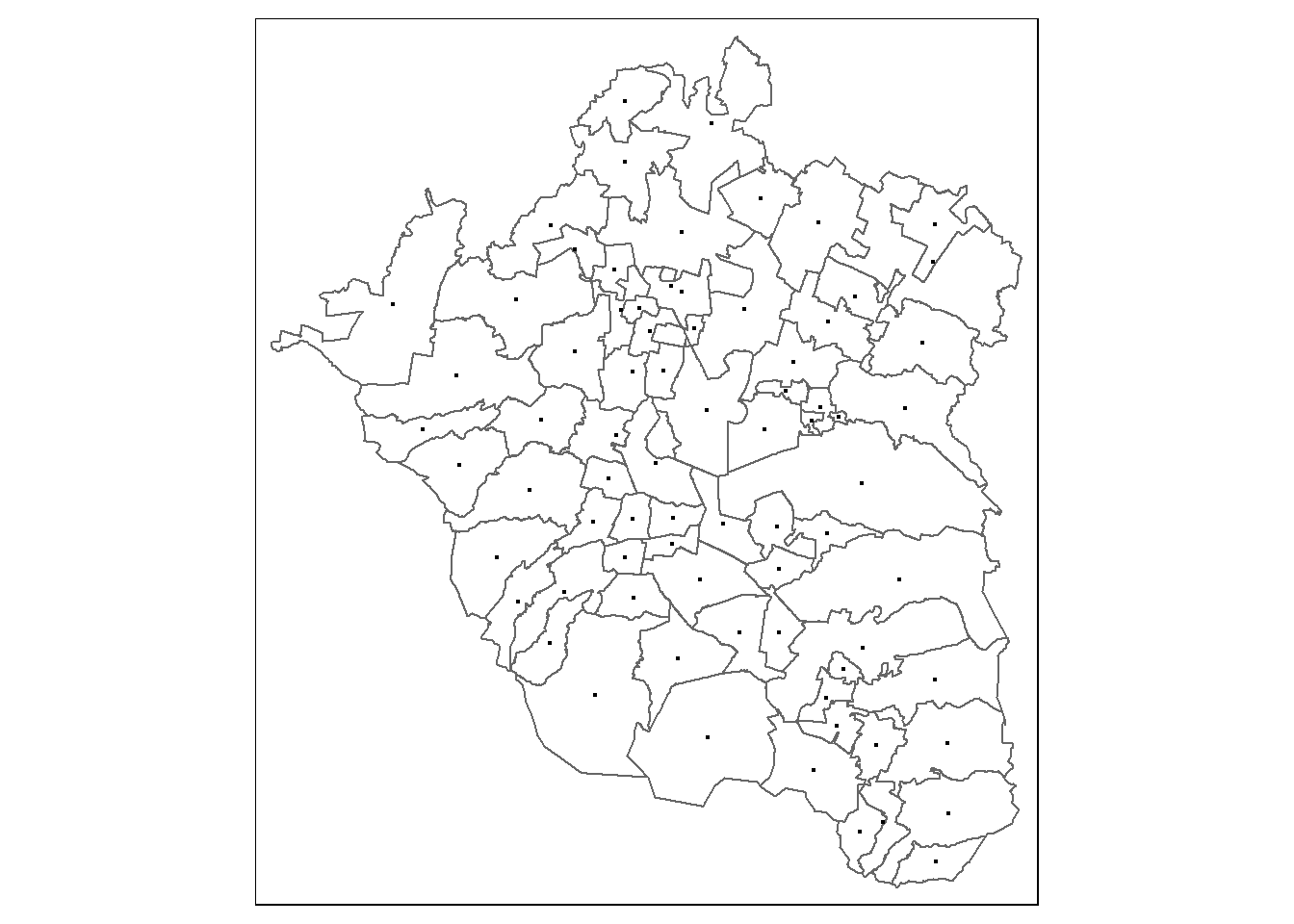

Como habrás podido notar, hemos agregado otra función que define la forma en que ha de representarse la capa de los centroides: tm_dots(). Ahí, es posible especificar la manera en que deseamos que aparezcan los centroides, por ejemplo, en color rojo y más grandes:

tm_shape(zmvm_cov_sf) +
  tm_borders() +
  tm_shape(zmvm_cntrds) +
  tm_dots(size=0.2,col="red")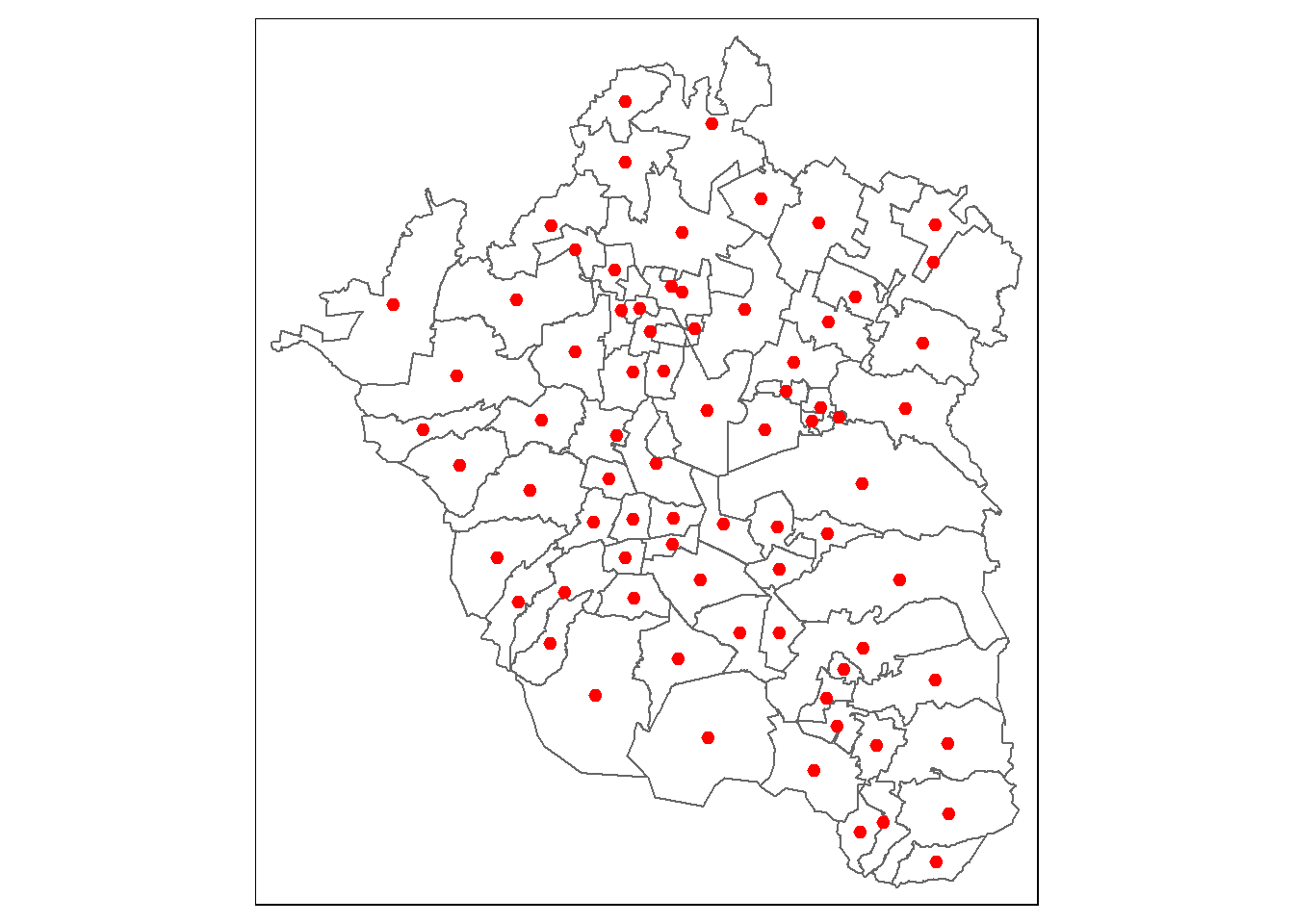

Para guardar la capa que contiene los centroides en un nuevo archivo SHP, usamos las siguientes líneas de código:

sf::st_write(obj=zmvm_cntrds, "zmvm_cntrds", driver = "ESRI Shapefile")

Como siempre, se recomienda revisar la documentación de ayuda de la función st_write() para conocer todos los detalles de los argumentos.

2.10 Tópico adicional: Mapas de clasificación especial (elementos de programación)

2.10.1 Una palabra de advertencia

En esta sección se construyen dos tipos de mapas de clasificación especial, es decir, destinados a hacer notar los valores atípicos. No obstante, la construcción de dichos mapas en R supone cierto conocimiento sobre programación que está fuera del alcance de estas notas. Si deseas profundizar en el aprendizaje de programación en R, el libro de Roger D. Peng, R Programming for Data Science es un excelente material, particularmente el capítulo 14 dedicado a las funciones en R (Roger D. Peng 2015).

Con esta advertencia, llevamos a cabo la exposición de esta sección, esperando motivarte para que tú misma profundices en los tópicos de programación.

2.10.2 Mapa de intervalos personalizados

Se señaló antes que, hasta donde tenemos conocimiento, en R no es posible construir mapas de clasificación especial con tmap a través de las opciones de estilo, no obstante, con algunos elementos de programación es posible solventar esta tarea. En esta sección nos servimos del código proporcionado por Luc Anselin y su equipo quienes, en un esfuerzo de difusión del conocimiento sobre el uso de estas herramientas, pone a nuestra disposición una basta cantidad de materiales en la página del Center for Spatial Data Science de la Universidad de Chicago (Anselin and Morrison 2018).

Para construir un mapa de intervalos definidos por el usuario, hay que recurrir al argumento breaks= dentro de la función tm_fill(). Para definir los intervalos de forma adecuada, se recomienda mirar las características resumen de la variable de interés, en este caso el número de casos positivos por COVID19 por cada mil habitantes, pos_hab:

summary(zmvm_cov_sf$pos_hab)

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   1.720   3.337   5.117   6.964   8.636  22.700

Esto nos permitirá conocer los valores que toma la variable de interés y pensar la manera en que deseamos delimitar las categorías de nuestro mapa. Supongamos que deseamos 6 categorías y, dado el rango de nuestra variable (valores entre 1.720 y 22.7), podemos fijar los cortes de los intervalos en 2.0, 6.0, 12., 18.0 y 24.0; además, se requiere incluir también un mínimo y máximo, digamos 1.0 y 25.0, para las categorías.

La información, tanto de los cortes como de los máximos y mínimos deber ser especifica en forma de vector: c(1.0, 2.0, 6.0, 12., 18.0, 24.0, 25.0). Debemos además especificar la paleta de colores que deseamos usar, atendiendo a lo dicho antes, usaremos una paleta con tres anclas: del amarillo, al naranja y al café, Yellow-Orange-Brown,YlOrBr:

tmap::tm_shape(zmvm_cov_sf) +
  tmap::tm_borders()+
  tmap::tm_fill("pos_hab",title="Casos positivos covid",breaks=c(1.0, 2.0, 6.0, 12., 18.0,  24.0, 25.0),palette="YlOrBr")+
  tm_layout(title = "Cortes personalizados", title.position = c("center","top"))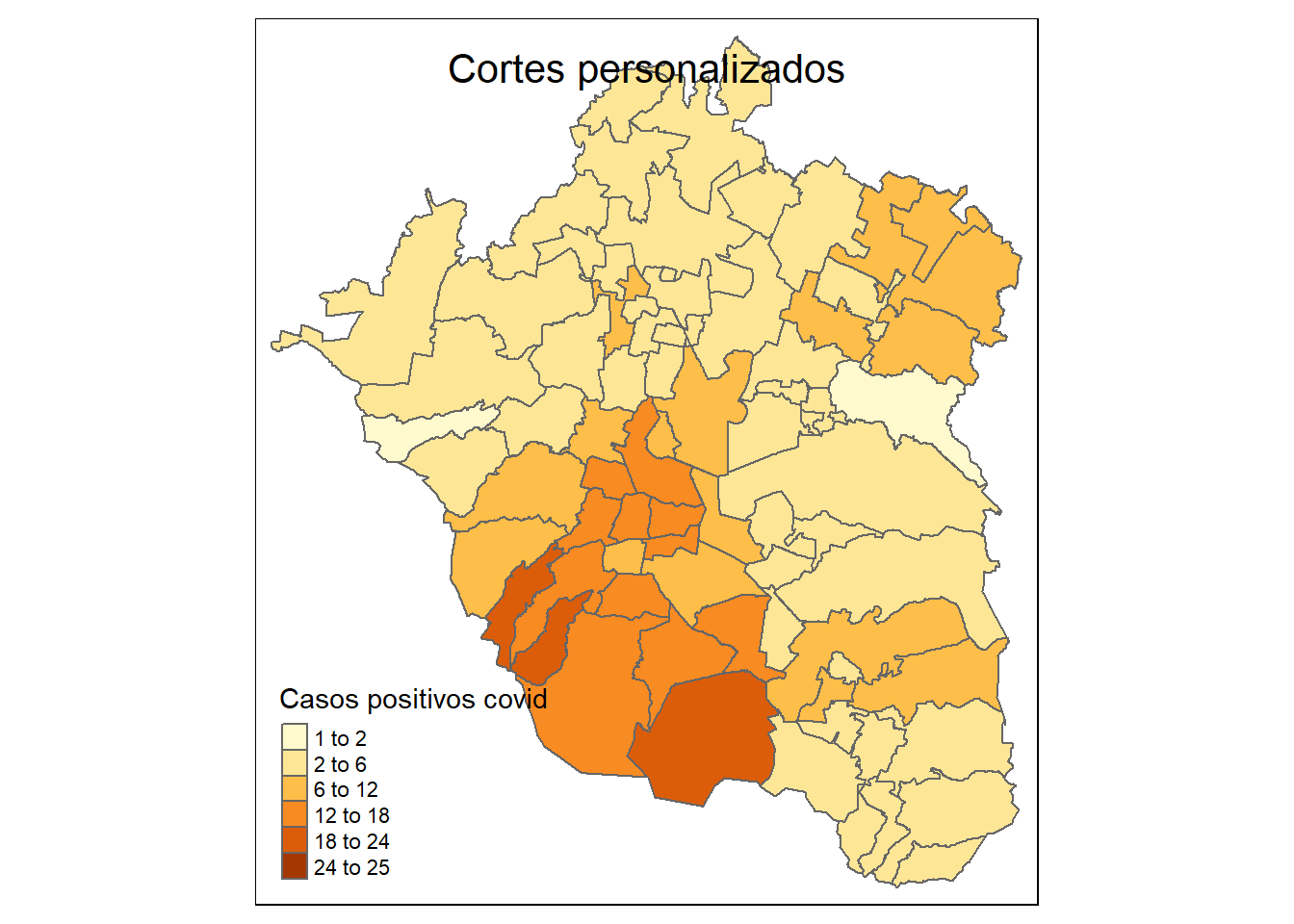

2.10.3 Mapas de valores extremos

2.10.3.1 Mapa de percentiles

Un mapa de percentiles es un tipo espacial de mapa de cuantiles en el que se especifican seis categorías: 0-1%,1-10%, 10-50%,50-90%,90-99% y 99-100%; de ellas las que interesan son las categorías que agrupan el 1% de los valores más bajos (0-1%) y el 1% de los valores más altos (99-100%), es decir, las observaciones extremas. Este tipo de mapas es útil, justamente, para identificar la localización de valores atíticos en el espacio. Para poder construirlo, en R debemos llevar a cabo los siguientes pasos:

1. Extraer la variable de nuestro arreglo de datos.
   
2. Calcular los percentiles de nuestro interés, es decir, 0.0,0.01,0.1,0.5,0.9,0.99,1.0.
   
3. Construir el mapa con base en los intervalos definidos a través de la función tm_fill().

Para el paso i, lo primero será construir una función que llamaremos get.var, que tendrá dos argumentos, varnom y df, el primero indicará, entre comillas, el nombre de la variable a utilizar y el segundo indicará la base de la que proviene. Esta función permite que, al extraer la variable de la base, se eliminen los “aspectos espaciales” asociadas a ella. Esta función sólo se requiere construir una vez.

get.var <- function(varnom,df) {#Definición de la función
  v <- df[varnom] %>% st_set_geometry(NULL) #Extracción de la variable de interés y remoción de sus características geográficas
  v <- unname(v[,1]) #Selección de la columna del data frame extraído que contiene la variable de interés y elimina su nombre pues sólo queremos un vector.
  return(v) #Resultado de la función: la variable como vector sin sus características espaciales
}

Ahora, echando mano de la función creada extraeremos la variable de interés sin sus aspectos espaciales:

pos_hab<-get.var("pos_hab",zmvm_cov_sf)
pos_hab

##  [1] 14.364996 16.983175 13.352654 16.163929 17.363687 17.313543 14.943518
##  [8] 17.404756 18.701249 13.677709 20.559563 10.224540 14.717256 22.700331
## [15] 11.088257  5.882283  4.938574  5.239423  2.570694  3.351482  4.267922
## [22]  2.382445  7.896182  2.088929  5.500198  5.891309  5.601076  9.197806
## [29]  8.113844  3.295057  3.676214  3.250036  3.583416  6.155522  2.124319
## [36]  2.787239  3.293624  6.120050  1.760416  5.184329  2.941489  3.873824
## [43]  2.507745  5.423064  7.354686  2.224869  3.992095  8.598203  6.385731
## [50]  4.385253  3.702180  3.693010  5.894044  4.147922  9.766454  3.853830
## [57]  5.546263  4.766342  8.751090  1.719690  3.024390  2.372319  2.380410
## [64]  3.876611  4.272596  7.134726  6.920539  5.049320  4.917293  2.582625
## [71]  3.918632  3.399002  2.473636  2.822012  6.913242 13.935302

Para el paso ii, hemos de crear un objeto en el que se guarden los percentiles de interés, un vector de 6 elementos:

percentiles <- c(0.0,0.01,0.1,0.5,0.9,0.99,1.0)

Ahora, se calculan y guardan valores de los percentiles con base en el par de objetos creados, percentiles y pos_hab, es decir, obtendremos los valores de la variable pos_hab en los percentiles de interés:

varperc <- quantile(pos_hab,percentiles)
varperc

##        0%        1%       10%       50%       90%       99%      100% 
##  1.719690  1.750234  2.428041  5.116824 15.553724 21.094755 22.700331

Ahora, en el paso iii, la construcción del mapa de percentiles es posible uniendo todos los elementos:

tmap::tm_shape(zmvm_cov_sf)+
  tmap::tm_fill("pos_hab",title="Índice de marginación 2010", breaks=varperc, palette="-RdBu",labels=c("< 1%", "1% - %10", "10% - 50%", "50% - 90%","90% - 99%", "> 99%"))+
  tmap::tm_borders() +
  tmap::tm_layout(title = "Mapa de percentiles", title.position = c("center","bottom"))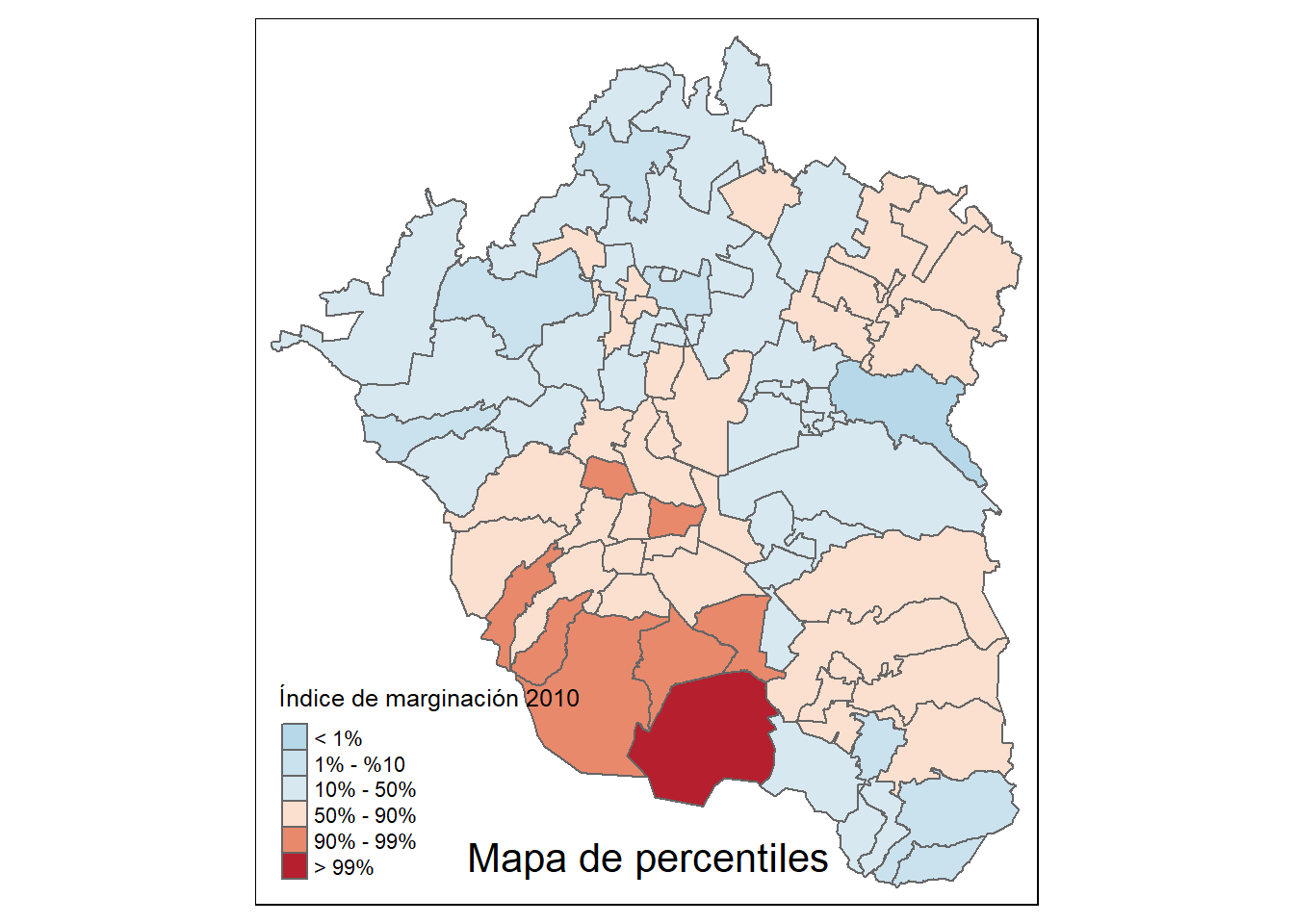

2.10.4 Construcción de una función personalizada para hacer mapas de percentiles

Con el camino que hemos seguido en la sección previa, es posible ahorrarnos muchos pasos y crear nuestra propia función (que opera en el entorno de trabajo activo de la sesión) para construir mapas de percentiles. Nuestra función se llamará percentmap() y tendrá los siguientes argumentos:

• varnom: nombre de la variable (especificada como texto entre comillas).
• df: base de datos que contiene el variable.
• legtitle: titulo de la leyenda del mapa.
• mtitle: título del mapa.

Para crear la función:

  percentmap <- function(varnom,df,titulo.leyenda=NA,titulo.principal="Mapa de percentiles"){ #Definición de la función y sus argumentos
  #Elementos preliminares
  percent <- c(0,.01,.1,.5,.9,.99,1) #Vector que contiene los percentiles de interés para el mapa
  var <- get.var(varnom,df) #Extracción de la variable de la base de datos con la función anterior
  varperc <- quantile(var,percent) #Cálculo de los percentiles de la variable extraída
  #Especificaciones del mapa
  tm_shape(df) +
     tm_fill(varnom,title=titulo.leyenda,breaks=varperc,palette="-RdBu", labels=c("< 1%", "1% - %10", "10% - 50%", "50% - 90%","90% - 99%", "> 99%"))  +
  tm_borders() +
  tm_layout(title = titulo.principal, title.position = c("center","bottom"))
}

La función que hemos creado para hacer nuestros mapas tiene cuatro argumentos: varnom,df,legtitle y mtitle. Los dos últimos tienen valores por omisión, lo que significa que no es necesario especificarlos al usar la función. Los dos primeros no tienen valor por omisión, por lo que será forzoso especificar dichos argumentos.

Ahora, invocando nuestra propia función e indicando los argumentos forzosos, varnom y df tenemos que:

percentmap("pos_hab",zmvm_cov_sf)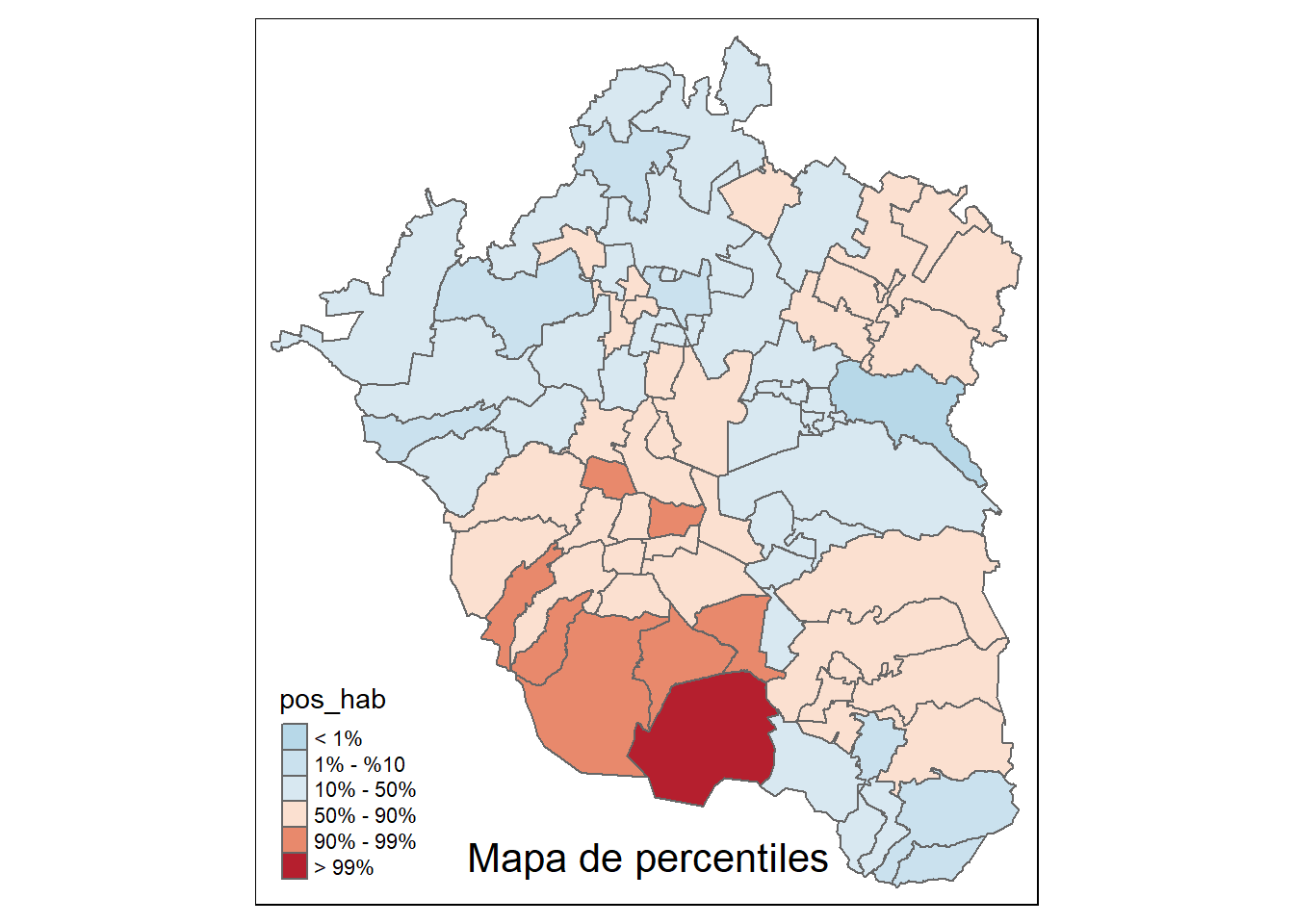

Podemos, como es obvio, cambiar los dos argumentos dados por omisión:

percentmap("pos_hab",zmvm_cov_sf, titulo.leyenda = "Categorías", titulo.principal = "El título que yo quiera" )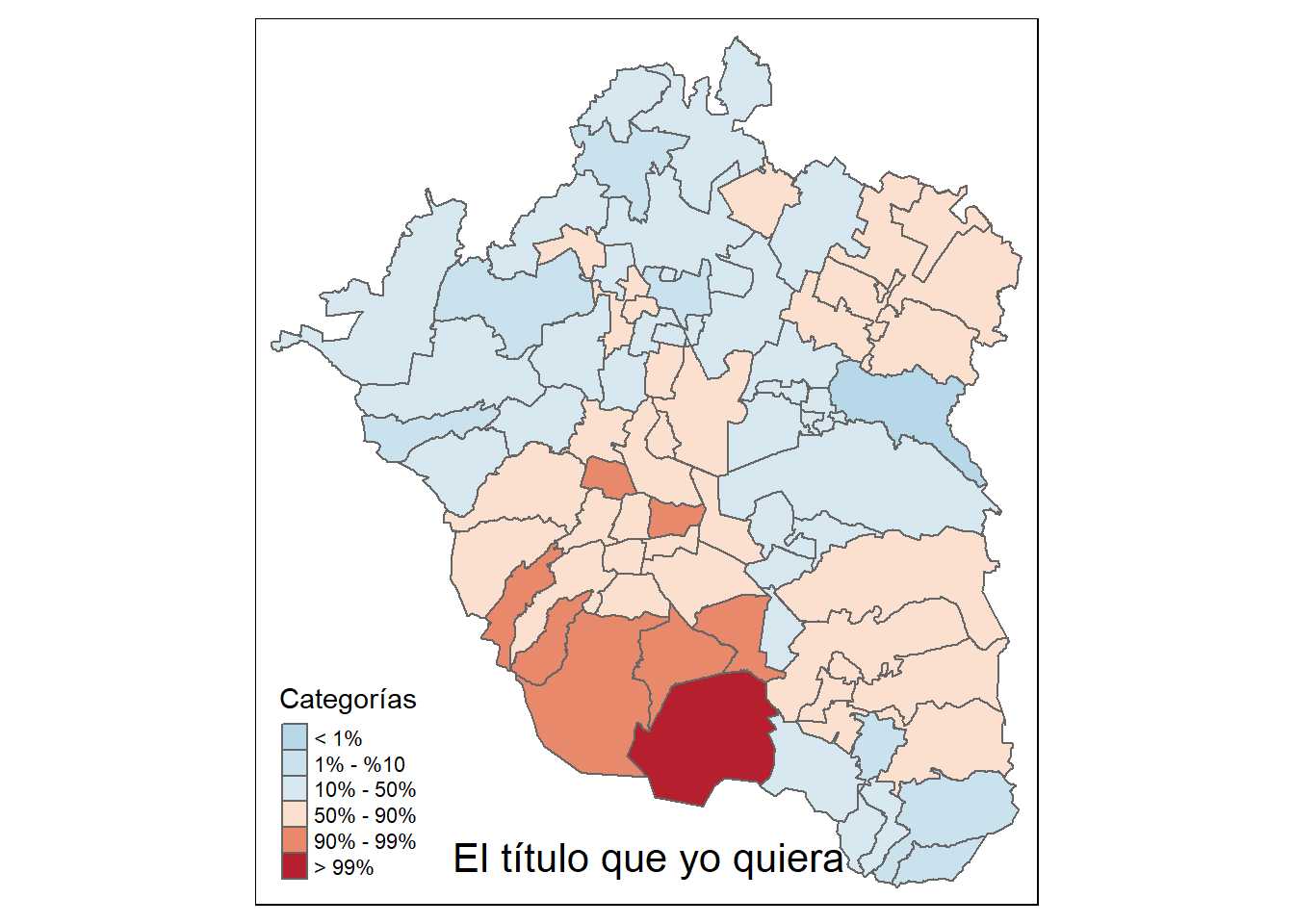

Los capítulos 1 y 2 de este libro, constituyen lo que suele ser denominado Análisis Exploratorio de Datos, (Exploratory Data Analysis, EDA). El capítulo 1 del e-Handbook of Statistical Methods expone con detalle esta concepción en el análisis de información (Croarkin and Tobias 2014). Además, en el capítulo 7 del ya citado libro R for Data Science también explica con detalle el enfoque EDA usando R.

En el siguiente capítulo continuamos con la exploración de la información, pero incorporando una estructura de relaciones en el espacio, por lo que a dicho enfoque se le conoce como Análisis Exploratorio de Datos Espaciales. En dicho capítulo será de nuestro interés particular un rasgo que suele estar presente en la información georreferenciada: la autocorrelación espacial.

"Análisis de datos espaciales con R" was written by Jaime Alberto Prudencio Vázquez. It was last built on 2023-10-05.

This book was built by the bookdown R package.