3 Análisis espacial I: autocorrelación
Observa el siguiente mapa. En él, se representa la variable índice de de desarrollo humano que calculó el Programa de Naciones Unidad para el Desarrollo (PNUD) en 2015.
## Reading layer `covid_zmvm' from data source
## `C:\repos\Analisis-de-datos-espaciales\base de datos\covid_zmvm shp\covid_zmvm.shp'
## using driver `ESRI Shapefile'
## Simple feature collection with 76 features and 57 fields
## Geometry type: MULTIPOLYGON
## Dimension: XY
## Bounding box: xmin: 2745632 ymin: 774927.1 xmax: 2855437 ymax: 899488.5
## Projected CRS: Lambert_Conformal_Conic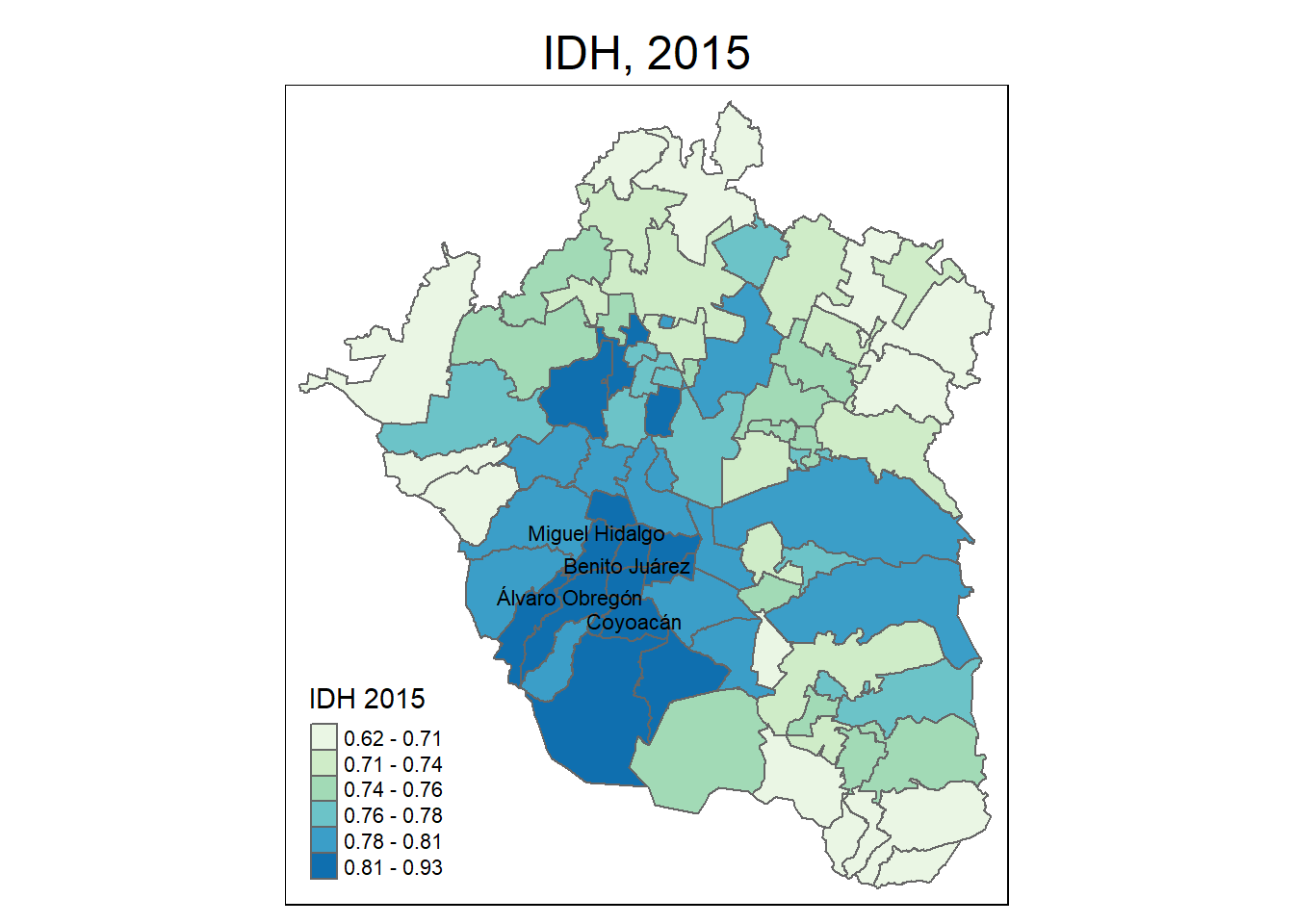
Figura 3.1. Índice de desarrollo humano para los municipios de la ZMVM, 2015
¿Notas algún patrón? ¿Detectas cómo los municipios con un valor alto del índice de desarrollo (Benito Juárez, Alvaro Obregón, Miguel Hidalgo, Coyoacán y otros) se encuentran agrupados en la parte centro-sur de la región considerada? Dicho patrón ilustra la posible presencia de autocorrelación espacial, es decir, que los valores de un indicador en una zona estén rodeados por valores muy semejantes o nada semejantes: en ambos casos decimos que hay autocorrelación. Cuando tratamos con datos de una variable georeferenciada hay altas probabilidades de que dicha variable esté autocorrelacionada y esto hace necesario que sean necesarias ciertas técnicas para su tratamiento, es decir, para su representación y modelación. En este capítulo trataremos con el concepto clave de autocorrelación espacial y veremos a través de que instrumentos es posible medirla para, más adelante, incorporar su riqueza informativa a una explicación sustantiva de los fenómenos socioterritoriales analizados.
3.1 Autocorrelación espacial y definición de vecindad
Una definición sintética de autocorrelación espacial es la que nos brinda Chasco (2003) como “la relación funcional existente entre los valores que adopta un indicador en una zona del espacio y en zonas vecinas” (Chasco 2003, 49). Por ejemplo, imagina que el barrio de la ciudad donde vives presenta un alto número de contagios por COVID19 y, además, los barrios vecinos tienen también valores altos: en este caso es probable que tengamos autocorrelación espacial positiva.
La identificación de autocorrelación espacial es importante como parte del proceso de análisis del fenómeno socioterritoriales al menos por dos cuestiones, una de carácter técnica durante la modelación econométrica y otra de carácter sustantiva en relación con la explicación del fenómeno. Respecto a la razón técnica, si existe autocorrelación espacial en nuestros datos lo más probable es que la estimación de los parámetros de un modelo con de mínimos cuadrados ordinarios deje de ser válida, en la medida en que no se cumplen los supuestos que requiere dicho procedimiento, específicamente, que los errores o perturbaciones del modelo no estén correlacionados; sobre esto abundaremos en el capítulo siguiente cuando hagamos un repaso de los modelos clásicos de regresión lineal.
Por otro lado, respecto a la razón sustantiva, emerge la pregunta, ¿qué pude estar ocurriendo que hace que un fenómeno aparezca, por ejemplo, agrupado en el espacio, es decir, que no se distribuya aleatoriamente en el territorio? ¿Por qué se concentra la actividad económica en determinadas ciudades o por qué algunos servicios sólo se brindan en una zona de la ciudad? Esto respecto a fenómenos económicos, pero ¿qué hay con el hecho de que una enfermedad se concentra notoriamente en algunas áreas de la ciudad y no en otras? Dicho en otras palabras, ¿qué hay detrás de la formación de un patrón en la forma en que se distribuye un fenómeno en el espacio y cómo puede ser esto explicado? A eso nos referimos cuando decimos que hay elementos sustantivos para el análisis al hallar evidencia de autocorrelación espacial.
Regresemos a la definición brindada de autocorrelación y analicémosla con más cuidado:
Relación funcional existente entre los valores que adopta un indicador en una zona del espacio y en zonas vecinas.
La definición se integra por tres elementos clave: i) valor de un indicador, ii) relación funcional y iii) zonas vecinas. Para dar sentido a nuestra definición pensemos en una afirmación como “los casos positivos de COVID19 en la alcaldía Azcapotzalco están asociados en forma directa con los casos positivos de COVID19 en las alcaldías y municipios vecinos que integran la Zona Metropolitana del Valle de México”. Tendríamos entonces que:
- Indicador: casos positivos por COVID19.
- Relación funcional: asociación positiva o directa.
- Zonas vecinas: alcaldías y municipios vecinos de Azcapotzalco.
El primer elemento no presenta dificultad alguna puesto que se refiere al valor de una variable en el espacio, tal y como la tenemos en la base de datos que hemos estado utilizando: casos positivos por COVID19 por cada 1 mil habitantes dentro de cuyas observaciones se encuentra Azcapotzalco; en tanto, el segundo elemento de nuestra afirmación es una mera suposición, es decir, que hay una relación positiva; por su parte, el tercer elemento “alcaldías y municipios vecinos” implica un problema: ¿de qué modo es posible establecer qué alcaldías son o no vecinas de Azcapotzalco?
Hay múltiples maneras que definir si un objeto espacial tiene o no vecinos, por ejemplo, podríamos decir que aquellas alcaldías que compartan límites administrativos con la demarcación territorial de nuestro interés serán sus vecinos (vecindad por adyacencia) o también sería posible establecer que las alcaldías vecinas serán aquellas que estén a menos de 10 km de distancia del centro económico de la alcaldía (vecindad por umbral de distancia) e incluso podríamos decir que las 3 alcaldías o municipios más cercanos serán los vecinos.
Ejercicio
¿Se te ocurre algún otro criterio para establecer vecindad?
¿Cómo llamarías a un criterio de vecindad donde elijas a los 3 vecinos más cercanos?
¿A partir de qué punto en el espacio será más conveniente medir la distancia, desde el centro económico de la alcaldía o municipio (por ejemplo su zona industrial o comercial) o desde la sede de la administración local?
¿La distancia más indicada usada como criterio de vecindad será una distancia lineal o una distancia por carretera?
Una vez que hemos visto que que existen diferentes criterios de vecindad, debemos pensar en una manera de almacenar dicha información. La Zona Metropolitana del Valle de México tiene 76 unidades espaciales, ¿de qué modo podemos apuntar todas las posibles relaciones de vecindad entre ellas? Las personas interesadas en el análisis espacial han propuesto un ingenioso instrumento matemático para captar y sintetizar cómo un objeto se relaciona con otros, es decir, para captar la estructura espacial del área de interés dada por las relaciones de vecindad. Dicho instrumento es denominado matriz de pesos espaciales; ilustremos esta idea. Piensa en un vecindario o área de estudio compuesto sólo por seis elementos, tal como se ilustra en la figura 3.2:
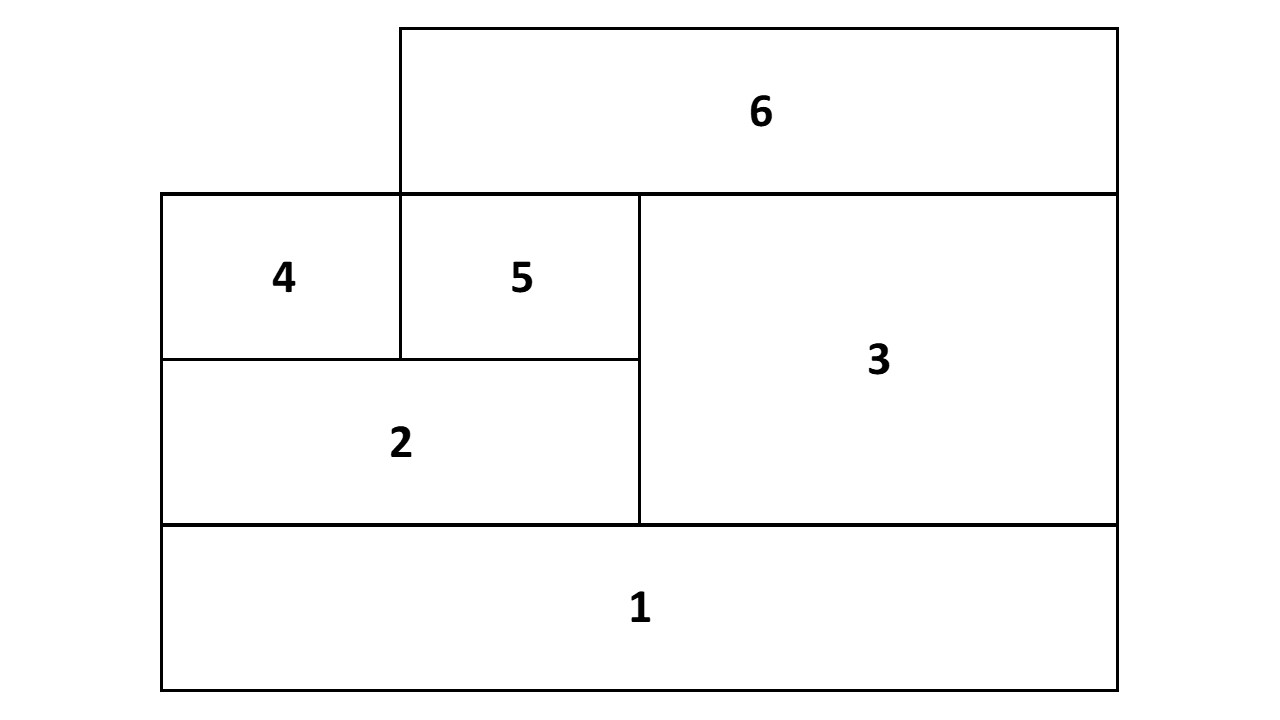
Figura 3.1: Vecindario regular
A partir de la disposición de este hipotético vecindario nos interesa construir una matriz de pesos espaciales, el instrumento para captar la estructura espacial de dicho vecindario. De los múltiples criterios de vecindad existentes, comencemos por el de adyacencia o contigüidad. A decir de Anselin (2020) “contigüidad significa que dos unidades espaciales comparten un borde común de longitud distinta de cero. Desde el punto de vista operativo, podemos distinguir entre un criterio de contigüidad de tipo torre y de tipo reina, en analogía con los movimientos permitidos para las piezas así nombradas en un tablero de ajedrez. El criterio de la torre define a los vecinos por la existencia de un borde común entre dos unidades espaciales. El criterio de la reina es algo más amplio y define a los vecinos como unidades espaciales que comparten un borde o un vértice comunes” (Anselin 2020).
De este modo, del criterio de vecindad por adyacencia tenemos dos tipos: torre y reina. Para construir nuestra matriz de pesos espaciales elijamos el criterio más amplio, de la reina. ¿Cómo podemos plasmar las relaciones de contigüidad entre los seis elementos de la figura 3.2? Pensemos en un cuadro que tiene tantas filas y columnas como objetos espaciales tiene nuestro vecindario, semejante al que aparece en la figura 3.3:
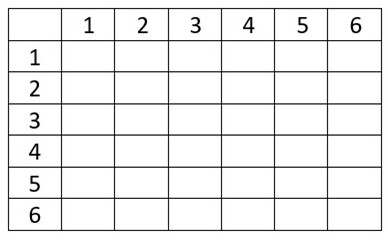
Figura 3.2: Matriz ejemplo vacía
Dicho cuadro será nuestra matriz de pesos espaciales y contendrá la estructura espacial del vecindario de la figura 3.2. Para un criterio de vecindad por adyacencia de tipo reina, ¿el elemento 1 y 2, son vecinos? Las unidades espaciales 1 y 2 de nuestro vecindario comparten un borde, por tanto, son vecinos y en el elemento (1,2) de nuestra matriz colocaremos un número 1; lo mismo ocurre entre las unidades espaciales 1 y 3 que, al compartir un lado, son vecinos y por tanto el elemento (1,3) de la matriz será también un 1. ¿Qué pasa entre los objetos 1 y 4? En este caso, no hay ni bordes ni vértices en común, por tanto, no hay una relación de vecindad, entonces, en el elemento (1,4) habremos de colocar un 0 que indica ausencia de vecindad. En síntesis, dado determinado criterio de vecindad, si dos objetos espaciales son vecinos, la relación de vecindad se indica mediante un número 1, en tanto, cuando no hay relación de vecindad su ausencia se indica colocando un 0. Hagamos esto para cada celda de la matriz hasta llenarla completamente y obtener algo parecido a lo que aparece en la figura 3.4.
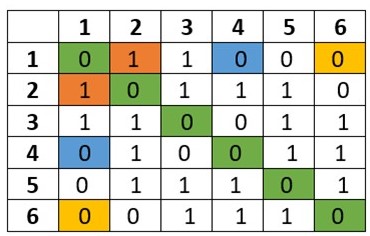
Figura 3.3: Matriz ejemplo llena
Resumamos lo dicho hasta este punto. El cuadro que acabamos de llenar es conocido como matriz de pesos espaciales5 y es el instrumento que nos permite sintetizar las relaciones espaciales o estructura de vecindad que corresponde a determinado criterio. Habrá, por tanto, diversos tipos de matrices en función del criterio de vecindad elegido. Esta matriz se denotada por la letra mayúscula \(W\) y está integrada por los elementos \(w_{ij}\) que toman el valor de 1 cuando el elemento \(j\) y el elemento \(i\) son vecinos y 0 (cero) en cualquier otro caso. Este instrumento es uno de los más importantes en econometría espacial ya que permite construir los estadísticos de autocorrelación espacial y es la manera en que podemos incorporar al espacio como variable a partir de lo que denominamos “rezago espacial”, como más adelante veremos en este y en el siguiente capítulo. Las características de la matriz de pesos espaciales son:
- Es una matriz que en la diagonal principal contiene sólo ceros, es decir, se asume que por definición no hay interacciones dentro de un mismo elemento (lo que no necesariamente es cierto y que dependerá de la escala de análisis).
- Es una matriz simétrica, es decir, se asume que hay interacción de “ida y vuelta”, por lo que con un instrumento de estas características no es posible asumir efectos de interacción en un solo sentido.
- Es una matriz cuadrada, es decir, de dimensiones \(n \cdot n\), donde \(n\) es el número de objetos espaciales.
Acabamos de ilustrar la lógica con la que puede ser construida una matriz de pesos espaciales a partir de una retícula regular con apenas seis elementos. Veamos ahora cómo obtener matrices de pesos espaciales sirviéndonos de R, ya que desarrollar los pasos anteriores para un vecindario compuesto por 76 objetos espaciales que son las alcaldías y municipios que integran el Valle de México es tarea para una máquina, no para nosotros.
3.2 Matrices de pesos espaciales en R
En R hay muchas rutas para desarrollar la misma tarea. Presentamos en este capítulo dos rutas: la primera se sirve del paquete spdep de Roger Bivand, en tanto que la segunda sigue la propuesta de Xun Li y su paquete rgeoda, una librería para llevar a cabo análisis espacial basado en la funcionalidades del software GeoDa.
3.2.1 Construcción de matrices con spdep
Roger Bivand y un equipo de colaboradores desarrollaron el paquete spdep para la construcción de matrices de pesos espaciales y el análisis espacial. En este enfoque la función poly2nb() nos permite calcular estructuras espaciales dadas a partir de dos tipos de vecindad por adyacencia, una más estricta (argumento queen=FALSE) y que la otra (argumento queen=TRUE). En la documentación de la función podemos leer que: “si es VERDADERO, TRUE, un solo punto límite compartido cumple la condición de contigüidad; si es FALSO, FALSE, se requiere más de un punto compartido; ten en cuenta que más de un punto límite compartido no significa necesariamente una línea límite compartida”. Además, para cargar la base de datos espacial recurriremos al paquete rgdal.
Lo dicho en el párrafo anterior es relevante en el sentido de que estos criterios no son exactamente los mismos que definimos antes (contigüidad reina y torre). Procedamos pues a la instalación de los paquetes, en caso de que aún no estén en nuestro sistema:
install.packages(c("spdep", "rgdal"))Primero, llamemos las librerías y carguemos la base de datos:
library(rgdal)
library(spdep)
covid_zmvm <-rgdal::readOGR("base de datos\\covid_zmvm shp\\covid_zmvm.shp")## OGR data source with driver: ESRI Shapefile
## Source: "C:\repos\Analisis-de-datos-espaciales\base de datos\covid_zmvm shp\covid_zmvm.shp", layer: "covid_zmvm"
## with 76 features
## It has 57 fieldsAhora, construyamos un objeto que llamaremos mTRUE, dicho objeto contendrá los elementos que definen la estructura espacial, es decir, será nuestra matriz de pesos espaciales. Esto lo haremos con la función poly2nb():
mTRUE <- spdep::poly2nb(covid_zmvm)El segmento de código anterior genera un objeto de tipo nb. Verifica sus características con class() y str() . Además, nota que en la sección de ambiente de trabajo (cuadrante superior derecho, en la pestaña ambiente) aparece el objeto creado. Da clic en la imagen de la lupa para visualizarlo e intenta interpretar el resultado de la ventana.
Ahora, llama al objeto y presta atención sobre los resultados que aparecen en la consola:
mTRUE## Neighbour list object:
## Number of regions: 76
## Number of nonzero links: 384
## Percentage nonzero weights: 6.648199
## Average number of links: 5.052632En la consola aparecen los siguientes elementos:
Objeto de lista de vecinos:
- Número de regiones: 76. Corresponde al número de alcaldías y municipios que componen la Zona Metropolitana del Valle de México.
- Número de enlaces distintos de cero: 380. Es el número de elementos de una matriz de 76x76 que registran relación de vecindad, dicho en otras palabras, es el total de números uno de la matriz.
- Porcentaje de pesos distintos de cero: 6.57. Resultado de dividir 380 entre (76x76).
- Número promedio de vínculos: 5. Número de vecinos que en promedio tiene cada municipio o alcaldía.
Ahora bien, para construir una lista de vecindad con base en un criterio más estricto, es decir, queen = FALSE, procedemos como:
mFALSE<- spdep::poly2nb(covid_zmvm, queen = FALSE)Ahora, llama dicho objeto y contrasta con los resultados anteriores.
mFALSE## Neighbour list object:
## Number of regions: 76
## Number of nonzero links: 372
## Percentage nonzero weights: 6.440443
## Average number of links: 4.894737Ejercicio
¿Qué objeto,
mTRUEomFALSE, tiene el mayor número de vínculos diferentes de cero?¿Por qué crees que esto es así?
Estas listas, que contienen nuestras estructuras espaciales almacenadas en los objeto de tipo nb llamados mTRUE y mFALSE, pueden representarse visualmente a través de un gráfico de conectividad que representa la estructura espacial definida por cada criterio a través de líneas que unen a los municipios considerados vecinos.
Para visualizar el mapa de conectividad recurriremos a la función plot() y se superpondran dos gráficas: una sólo con los bordes o límites a nivel municipal y otra con los centroides y la estructura espacial. Aquí se muestra el mapa de conectividad resultado de la matriz mTRUE
plot(covid_zmvm, border = 'lightgrey')
plot(mTRUE, coordinates(covid_zmvm), add=TRUE, col='lightblue')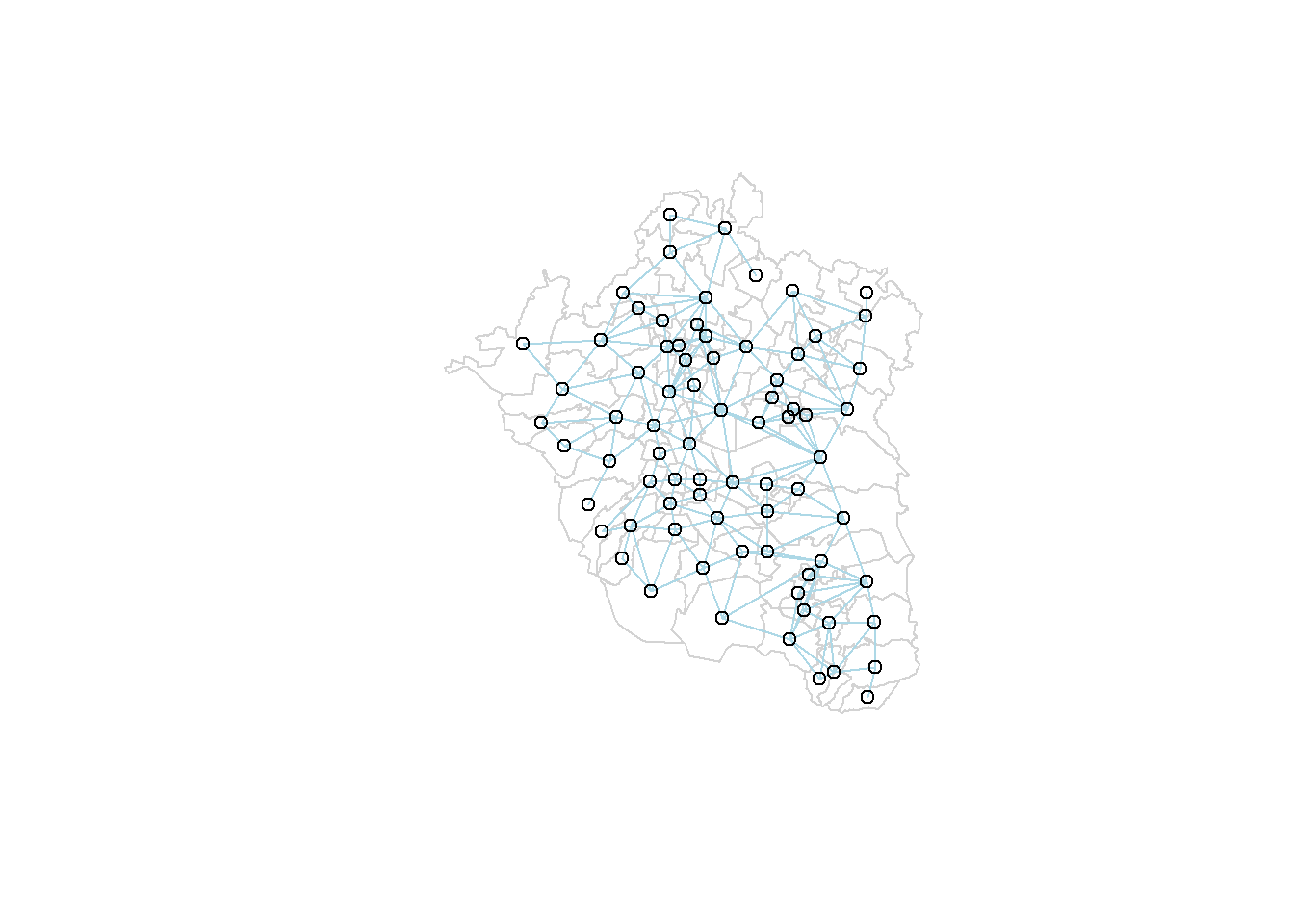
Para comparar ambas estructuras espaciales, mTRUE y mFALSE podemos superponer las dos gráficas y asignar colores diferentes:
plot(covid_zmvm, border = 'lightgrey')
plot(mTRUE, coordinates(covid_zmvm), add=TRUE, col='blue')
plot(mFALSE, coordinates(covid_zmvm), add=TRUE, col='lightgreen')
Como puedes observar, son estructuras muy parecidas, aunque aun así es posible notar sus diferencias.
3.2.2 Construcción de matrices con rgeoda
A diferencia del enfoque previo, con el paquete rgeoda es necesario cargar la base de datos espacial a través del paquete sf. Si no los has instalado:
install.packages(c("rgeoda", "sf"))Para cargarlos:
Ahora bien, carguemos la base de datos espacial con sf:
covid_zmvm_sf <- sf::st_read("base de datos/covid_zmvm shp/covid_zmvm.shp")## Reading layer `covid_zmvm' from data source
## `C:\repos\Analisis-de-datos-espaciales\base de datos\covid_zmvm shp\covid_zmvm.shp'
## using driver `ESRI Shapefile'
## Simple feature collection with 76 features and 57 fields
## Geometry type: MULTIPOLYGON
## Dimension: XY
## Bounding box: xmin: 2745632 ymin: 774927.1 xmax: 2855437 ymax: 899488.5
## Projected CRS: Lambert_Conformal_ConicEjercicio
Observa tu ambiente de trabajo (ventana superior derecha, en la pestaña “ambiente”). ¿De qué tipo es el objeto
covid_zmvm_sfy de cuálcovid_zmvm?¿A qué crees que se deban dichas diferencias?
A través del paquete rgeoda es posible construir, como en GeoDa, cuatro tipos de matrices de pesos:
- Matrices basadas contigüidad
- Matrices basadas en distancia
- Matrices de k-vecinos más cercanos
- Matrices de pesos por kernel
De ellas, aquí construiremos sólo las tres primeras.
3.2.2.1 Matrices basadas en contigüidad
En rgeoda hay dos matrices de pesos espaciales basadas en contigüidad, tal y como lo expisimos en la primera sección de este capítulo, las de tipo reina y las de tipo torre. Para construir una matriz de tipo reina recurrimos a la función queen_weight() y para una de tipo torre usamos rook_weights(), ambas funciones tienen cuatro argumentos:
-
sf_obj=: nuestra cartografía en formato sf, tal y como la hemos ya cargado.
-
order=: orden de contigüidad, donde si es igual a 1 se indica que sólo los objetos espaciales inmediatos serán vecinos y si es mayor que uno indicará una vecindad de orden superior (si es 2 indica que los vecinos de mis vecinos serán mis vecinos, si es tres los vecinos de mis vecinos de mis vecinos serán mis propios vecinos, y así sucesivamente).
-
include_lower_order=: indica si los vecinos de ordenes inferiores incluidos en la estructura de vecindad.
-
precision_threshold=: este argumento modifica la precisión de la geometría y se usará en caso de que, no habiendo observaciones aisladas, se detecte que algún objeto no tiene vecinos.
| Ejercicio |
| Ve a la ayuda de la funciones y responde: |
| i. ¿Qué argumentos son obligatorios? ii. ¿Cuáles opcionales? |
Así, para construir la matriz de tipo reina:
queen_w <- rgeoda::queen_weights(covid_zmvm_sf)En tanto, una matriz de contigüidad con el criterio de tipo torre::
rook_w <- rgeoda::rook_weights(covid_zmvm_sf)Los objetos recién creados y que contienen las estructuras de vecindad pueden ser grabadas en un archivo fuera del ambiente del trabajo, para hacerlas permanentes. Para ello usamos la función save_weights(), esta función tiene cuatro argumentos obligatorios: nombre de la matriz a hacerse permanente (gda_w=), el identificador único para cada objeto espacial (id_variable=), la ruta donde se almacenará el archivo de salida y el nombre del archivo (out_path=) y el nombre de la capa de entrada (layer_name=):
#Para la matriz reina
rgeoda::save_weights(gda_w=queen_w,
id_variable=covid_zmvm_sf['cvemun'],
out_path = 'base de datos/covid_zmvm shp/q_1.gal',
layer_name = 'covid_zmvm_sf')## [1] TRUE
#Para la matriz toree
rgeoda::save_weights(rook_w,
covid_zmvm_sf['cvemun'],
out_path = 'base de datos/covid_zmvm shp/r_1.gal',
layer_name = 'covid_zmvm_sf')## [1] TRUESi bien se dijo antes, en la sección dedicada a comentar qué es una matriz de pesos espaciales, que se definía la estructura espacial a través de una matriz, computacionalmente esto no es así, como seguro habrás notado al tratar de leer las matrices construidas con spdep en la sección anterior. Identifica los archivos creados con las funciones previas, en la sección de archivos en la sección inferior derecha (pestaña files) y selecciona q_1.gal. Notarás que, en efecto, el archivo no es una matriz, sino una lista. El hecho de que se usen listas y no matrices para el proceso de cómputo de las estructuras espaciales es porque las listas son más conveniente en términos de la cantidad ocupada de recursos del sistema. La razón detrás de ello es que las matrices de pesos espaciales son matrices dispersas, es decir, matrices que contienen muchos elementos que son cero.
Del archivo que acabas de abrir, q_1.gal, veámos con detenimiento su contenido para comprender mejor cómo se almacena la información. Reproducimos en seguida las tres primeras líneas:
09010 | 5 | | | |
09014 | 09008 | 09016 | 09003 | 09012 |
- Línea 1: en la primera columna aparece el número de objetos espaciales (76), en la segunda columna el nombre del archivo del que proviene la estructura (covid_zmvm_sf) y en la tercera la clave de identificación única para cada objeto (cvemun).
- Línea 2: en la primera columna se indica el objeto espacial su clave (09010), mientras que en la segunda columna se indica el número de vecinos que dicho objeto tiene, en este caso, cinco.
- Línea 3: en esta fila aparece, para cada columna, la clave de identificación de los cinco vecinos de 09010: 09014 09008 09016 09003 09012.
El resto de las líneas tiene la misma interpretación que las líneas 2 y 3: número de vecinos del objeto listado e identificación de los vecinos. Una vez que hemos comprendido la estructura de dicho archivo, pidamos un resumen del objeto queen_w:
summary(queen_w)## name value
## 1 number of observations: 76
## 2 is symmetric: TRUE
## 3 sparsity: 0.0616343490304709
## 4 # min neighbors: 1
## 5 # max neighbors: 9
## 6 # mean neighbors: 4.68421052631579
## 7 # median neighbors: 4
## 8 has isolates: FALSEDe dicho resumen es posible apuntar que: nuestro vecindario, la Zona Metropolitana del Valle de México, tiene 76 unidades espaciales (number of observations), la matriz construida es simétrica (is symmetric: TRUE), los municipios y alcaldías tienen al menos un vecino (# min neighbors: 1), el número máximo de vecinos es de 9 (# max neighbors: 9), la media de 4.68 (# mean neighbors), la mediana de 4 (# median neighbors) y que no hay observaciones sin vecinos (has isolates: FALSE). El elemento que no hemos indicado es sparsity: que tiene un valor de 0.0616. Dicho valor corresponde a la proporción de elementos diferentes a cero en una matriz de 76x76 objetos, es decir, nuestra matriz sólo tiene 6.16% son diferentes de cero.
3.2.2.2 Matrices basadas en distancia
En `rgeoda`` hay dos tipos de matrices que recurren a la distancia: la matriz de úmbral de distancia mínima y la matriz de k-vecinos más cercanos. Para el caso de la matriz de umbral, se considera que dos objetos espaciales, en el caso aquí analizado, dos municipios o alcaldías, son vecinos siempre que estén dentro de cierto umbral de distancia dado. Para el caso de la matriz de k-vecinos más cercanos, la idea es que un objeto espacial tendrá como vecinos a los k-objetos más cercanos.
3.2.2.2.1 Matriz basada en umbral distancia
Para construir una matriz de pesos espaciales basada este criterio tenemos proceder en dos pasos: i) definir un umbral de distancia mínimo en el cual todas las unidades espaciales tienen al menos un vecino, ii) usar dicho umbral para hallar cada uno de los vecinos, dado ese umbral.
Para definir el umbral usamos la función min_distthreshold() del paquete `rgeoda``:
umbral <- rgeoda::min_distthreshold(covid_zmvm_sf)
umbral## [1] 13943.63La distancia mínima para que cada uno de los 76 municipios y alcaldías tenga un vecino es 13,943.63 metros. Sabemos que las unidades del resultado anterior son metros puesto que en el archivo con extensión .prj (el archivo que contiene la información sobre la proyección cartográfica utilizada) así se indica. Ahora bien, definido el umbral ya podemos construir la matriz:
dist_w <- rgeoda::distance_weights(covid_zmvm_sf, umbral)
summary(dist_w)## name value
## 1 number of observations: 76
## 2 is symmetric: TRUE
## 3 sparsity: 0.0772160664819945
## 4 # min neighbors: 1
## 5 # max neighbors: 11
## 6 # mean neighbors: 5.86842105263158
## 7 # median neighbors: 5.5
## 8 has isolates: FALSE3.2.2.2.2 Matriz de k-vecinos más cercanos
Cuando decimos k-vecinos más cercanos, con ello queremos decir que se identificará determinado número “k” de vecinos más cercanos: los 2 más cercanos (k=2), los 8 más cercanos (k=8), etcétera. Para ello nos servimos de la función knn_weights(). Si quiseramos una matriz con los 4 vecinos más cercanos, tenemos que:
k4_w <- knn_weights(covid_zmvm_sf, 4)
summary(k4_w)## name value
## 1 number of observations: 76
## 2 is symmetric: FALSE
## 3 sparsity: 0.0526315789473684
## 4 # min neighbors: 4
## 5 # max neighbors: 4
## 6 # mean neighbors: 4
## 7 # median neighbors: 4
## 8 has isolates: FALSEA diferencia de las matrices anteriores, ésta no es simétrica y, como te podrás dar cuenta, hace que cada objeto espacial tenga exactamente el mismo número de vecinos, en este caso, cuatro.
3.3 Variables espacialmente rezagadas
La construcción de un rezago espacial, también llamada variable espacialmente rezagada, es un elemento clave para poder operacionalizar y, por tanto, medir la autocorrelación. Pero, ¿qué es un rezago espacial? Imagina que vives en un barrio de la Ciudad de México que tiene 8 barrios vecinos, mismos que calculaste con alguno de los criterios de que vimos antes y que apuntaste en una matriz de pesos espaciales. Supón ahora que tu barrio tiene 5 casos de COVID19 y quieres comparar dicho dato con el de los 8 barrios vecinos, ¿cómo lo harías? Una alternativa útil es sintetizar la información de los ocho barrios en un sólo indicador que sume y pondere los datos de los casos positivos de los vecinos.
Veamos esto con más cuidado y definamos formalmente rezago espacial. Antes dijimos que cada uno de los elementos \(w_{ij}\) de la matriz de pesos espaciales \(W\) pueden tomar como valores ceros o unos. La matriz \(W\) puede escribirse como:
\[ W= \begin{pmatrix} w_{11} & w_{12} & \cdots & w_{1n}\\ w_{21} & w_{22} & \cdots & w_{2n}\\ \vdots & \vdots & \ddots & \vdots \\ w_{n1} & w_{n2} & \dots & w_{nn}\\ \end{pmatrix} \]
No obstante, es posible expresar dicha matriz \(W\) de una forma diferente, normalizandola por filas. Normalizar una matriz de pesos espaciales por filas implica dividir cada elemento \(w_{ij}\) de una fila entre la suma de elementos diferentes a cero de dicha fila, por lo que los elementos de una matriz de pesos espaciales estandarizada por fila es:
\[w_{ij(s)}=\frac {w_{ij}} {\sum{w_{ij}}}\] Nuestra matriz de pesos espaciales estandarizada por filas, \(W_s\), es pues una transformación de la matriz original que hace que todas las filas sumen en total 1:
$$ w_{11(s)} + w_{12(s)} + + w_{1n(s)}= 1\ w_{21(s)} + w_{22(s)} + + w_{2n(s)}=1\ w_{n1(s)} + w_{n2(s)} + + w_{nn(s)}=1
$$
Regresemos a nuestra definición sobre la autocorrelación espacial: relación funcional existente entre los valores que adopta un indicador en una zona del espacio con respecto al valor de sus zonas vecinas, dicho valor es lo que llamamos rezago espacial. Así pues, un rezago espacial es definido como el promedio ponderado del valor de la variable de los vecinos (Chasco 2003, 61; Anselin 2020). Siguiendo a Anselin (2020), “el rezago espacial de \(y\) del objeto espacial \(i\) es expresado como \(Wy_{i}\):
\[ \begin{aligned} Wy_i &= w_{i1(s)}y_1+w_{i2(s)}y_2+...+w_{in(s)}y_n \\ Wy_i &= \sum_{j=1}^nw_{ij(s)}y_j \\ \end{aligned} \]
Donde \(w_{ij(s)}\) es cada uno de los elementos de la matriz de pesos estandarizada por fila y \(y_n\) es el valor de la variable de interés. Así pues, el rezago espacial pondera la variable de interés a través del número de vecinos que cada unidad espacial posee.
De nueva cuenta, es posible construir rezagos espaciales ya sea con el paquete spded o rgeoda. Primero ilustraremos la alternativa con spdep y en seguida con rgeoda.
3.3.1 Rezagos espaciales con spdep
Para construir con spdep el rezago espacial de una variable, digamos de los casos positivos por COVID19, debemos primero estandarizar los objetos que contienen las estructuras espaciales que previamente construimos: mTRUE y mFALSE. Este proceso corre a cuenta de la función nb2listw() del paquete spdep:
mTRUE.est <- spdep::nb2listw(mTRUE)
mTRUE.est## Characteristics of weights list object:
## Neighbour list object:
## Number of regions: 76
## Number of nonzero links: 384
## Percentage nonzero weights: 6.648199
## Average number of links: 5.052632
##
## Weights style: W
## Weights constants summary:
## n nn S0 S1 S2
## W 76 5776 76 35.56142 319.6623
mFALSE.est <- spdep::nb2listw(mFALSE)
mFALSE.est## Characteristics of weights list object:
## Neighbour list object:
## Number of regions: 76
## Number of nonzero links: 372
## Percentage nonzero weights: 6.440443
## Average number of links: 4.894737
##
## Weights style: W
## Weights constants summary:
## n nn S0 S1 S2
## W 76 5776 76 36.56499 319.6716Notaras cómo en el ambiente de trabajo se ha creado un objeto nuevo de tipo listw. Ábrelo y observa su contenido.
Ejercicio
¿Explica por qué se le denomina matriz (lista) estandarizada?
¿A cuanto es igual la suma de cada renglón de la lista?
¿Cómo se relaciona la forma en que aparecen enlistados los elementos con el número de vecinos que tiene cada objeto espacial?
Construiremos un rezago espacial de la variable pos_hab, número de casos positivos por COVID19, con ayuda de la función lag.listw() del paquete spdep. Indicamos dos argumentos en la función: la estructura espacial dada por la matriz estandarizada, mTRUE.est, y la variable de la que deseamos el rezago espacial, pos_hab, esto es guardado en un nuevo objeto, lag_poshab, tal y como se muestra en el siguiente segmento de código:
lag_poshab <- spdep::lag.listw(mTRUE.est, covid_zmvm$pos_hab)Para lograr apreciar mejor el rezago espacial, construiremos una tabla de dos columnas que almacenaremos en el objeto df, la primera contendrá la variable original y la segunda el rezago espacial, luego pediremos que nos muestre los primeros registros de la tabla con la función head() en un formato estilizado a través de la función kable() del paquete knitr:
#Crea un nuevo arreglo de datos donde se almacena la variable original y el rezago espacial
df <- base::data.frame(pos_hab = covid_zmvm$pos_hab, lag_poshab)
library(knitr)
#Coloca los primeros valores de ambas variables en una tabla, requiere instalación y carga del paquete knitr
kable(head(df))| pos_hab | lag_poshab |
|---|---|
| 14.36500 | 15.99225 |
| 16.98318 | 16.81821 |
| 13.35265 | 14.48267 |
| 16.16393 | 12.22961 |
| 17.36369 | 12.18342 |
| 17.31354 | 11.97155 |
El valor de la segunda columna, lag_poshab, es el rezago espacial. ¿Cómo interpretamos dicho valor? Veamos con cuidado. El primer valor listado de pos_hab, 14.365, es el número de casos positivos de COVID19 por cada 1 mil habitantes y dicho valor pertenece a la alcaldía Álvaro Obregón, en tanto, el primer valor listado en la columna lag_poshab es el rezago espacial y asciende a 15.992, este valor es el promedio ponderado de casos positivos por COVID19 en los vecinos Álvaro Obregón.
Para identificar a los vecinos de cada objeto espacial (municipio o alcaldía), así como el respectivo valor del rezago espacial hay que extraer dicha información utilizando una notación de dobles corchetes. Vayamos por pasos. Primero, para conocer cual es el primer elemento u objeto espacial de nuestra base usamos la notación del doble corchete sobre el objeto covid_zmvm:
covid_zmvm$nom_mun[[1]] #Devuelve el nombre del municipio identificado con el número 1## [1] "Álvaro Obregón"Una vez que sabemos que dicho objeto es la alcaldía llamada Álvaro Obregón, pidamos a R que nos muestre cuáles son sus vecinos. Para ello, usando de nuevo la notación de doble corchete sobre la estructura espacial, el objeto mTRUE:
mTRUE[[1]]#Devuelve los números de identificación de los municipios y alcaldías vecinas del Álvaro Obregón, la observación identificada con el número 1.## [1] 2 7 9 10 11 15Los números anteriores corresponden a los vecinos de Álvaro Obregón, pero, ¿cómo saber su nombre y el número de casos positivos de cada uno? El siguiente segmento de código nos dará los nombres de los vecinos y el número de casos positivos en cada uno.
#Crea un objeto que contiene el nombre de las alcaldías y municipios vecinos de Álvaro Obregón
Alcaldías <- covid_zmvm$nom_mun[mTRUE[[1]]]
#Crea un objeto que contiene el valor de la variable pos_hab (casos positivos por mil habitantes) para cada observación vecina de Álvaro Obregón
Casos_covid <- covid_zmvm$pos_hab[mTRUE[[1]]]
# Guarda los dos objetos anteriores en un dataframe y lo muestra en una tabla
db <- data.frame(Alcaldías, Casos_covid)
kable(db)| Alcaldías | Casos_covid |
|---|---|
| Tlalpan | 16.98318 |
| Coyoacán | 14.94352 |
| Cuajimalpa de Morelos | 18.70125 |
| Miguel Hidalgo | 13.67771 |
| La Magdalena Contreras | 20.55956 |
| Benito Juárez | 11.08826 |
Los valores previamente listados corresponden tanto al nombre como al número de casos positivos de los vecinos de Álvaro Obregón. Así, el rezago espacial de Álvaro Obregón es el resultado de sumar los valores de la tabla anterior y multiplicarlos por \(\frac {1}{6}\), es decir, 15.99.
Ejercicio
¿Por que para el caso de Álvaro Obregón hubo que multiplicar por un sexto?
Obtén un cuadro con las lista de vecinos y los valores de casos positivos para el objeto espacial 35
3.3.2 Rezagos espaciales con rgeoda
Con el paquete rgeoda calcular rezagos espaciales es sencillo con la función spatial_lag(), en la que hay que especificar dos argumentos: gda_w= la matriz de pesos espaciales y df= la variable sobre la que se desea el rezago espacial, que proviene del objeto de tipo sf. Por ejemplo, para la variable casos positivos, pos_hab y con una matriz de tipo reina, queen_w:
lag <- rgeoda::spatial_lag(queen_w,
covid_zmvm_sf['pos_hab'])
head(lag)## Spatial.Lag
## 1 15.45044
## 2 15.57109
## 3 13.91179
## 4 12.22961
## 5 13.20082
## 6 11.51118Para mejor mirar el rezago espacial, incorporémoslo a un nuevo dataframe con la variable pos_hab, de forma emejante a como lo hicimos antes:
df <- base::data.frame(pos_hab = covid_zmvm_sf$pos_hab, lag)
kable(head(df))| pos_hab | Spatial.Lag |
|---|---|
| 14.36500 | 15.45044 |
| 16.98318 | 15.57109 |
| 13.35265 | 13.91179 |
| 16.16393 | 12.22961 |
| 17.36369 | 13.20082 |
| 17.31354 | 11.51118 |
Ejercicio
Con el paquete
rgeoda, construye rezagos espaciales con las otras estructuras espaciales: torre, distancia mínima, k-vecinos.¿Por qué en cada caso es diferente el valor rezago?
3.4 Coeficiente de correlación espacial: la I de Moran
Una vez que hemos abordado y resuelto el problema de cómo definir vecindad a partir de la matriz de pesos espaciales y que hemos operacionalizado la definición de valor de la variable en los vecinos a través de la noción de rezago espacial, tenemos todos los elementos que integran la definición de autocorrelación espacial: i) relación funcional, ii) valor de una variable y iii) relación de vecindad.
Ahora bien, ¿cómo medimos la autocorrelación? Es decir, cómo sabemos si, por ejemplo, la variable casos positivos por COVID19 está autocorrelacionada. Al principio de este capítulo dijimos que apreciar ciertos patrones de agrupamiento en un mapa, como el del índice de desarrollo humano, era un posible indicio de autocorrelación espacial. Es momento de formalizar dicho indicio a través de un indicador apropiado. Debemos pues construir un estadístico, un estadístico de autocorrelación espacial.
El estadístico de asociación espacial más socorrido es el propuesto por Patrick Moran: la I de Moran. La I de Moran es un coeficiente de correlación lineal que “incorpora al espacio”, es decir, mide la asociación lineal entre una variable (digamos casos positivos por COVID19) y su rezago espacial (el valor promedio de los casos positivos de los vecinos). Como todo coeficiente de asociación, el valor de la I de Moran se encuentra entre -1 y 1.
Si el valor de la I de Moran es positivo decimos que hay signos de concentración o patrones de aglomeración pues existe autocorrelación espacial positiva, por lo que existen unidades espaciales (alcaldías, municipios) que tienen valores altos en la variable medida que están rodeadas por otras unidades espaciales que tienen valores también altos. Decir que existe autocorrelación espacial positiva también implica afirmar que hay unidades espaciales con valores bajos rodeadas de otras que tienen también valores bajos.
Por otro lado, si la I de Moran es negativa esto es evidencia de otro tipo de patrones, ya no de aglomeración sun ode dispersión o repulsión: una alcaldía o municipio que tiene valores altos está rodeada de vecinos con valores bajos y viceversa.
Hasta donde sabemos, el paquete rgeoda aún no incorpora una función para construir automáticamente la I de Moran, por lo que el enfoque aquí presentado corresponde, para simplificar, al del paquete spdep.
Para calcular en R el coeficiente o estadístico de Moran necesitamos recurrir a la función moran.test() del paquete spdep. Los argumentos de la función deben especificar el nombre de la variable y el tipo de estructura espacial dado por la matriz de pesos usada; adicionalmente, se puede indicar qué hacer en caso de que existan islas (objetos espaciales sin vecinos) con el argumento zero.policy.
Ejercicio
Solicita ayuda del paquete
spdepy responde, ¿para qué sirve el argumentorandomizationde la funciónmoran.test()?De nuevo, en la ayuda de la función, ¿con cuál de los argumentos es posible cambiar la hipótesis alternativa de la evaluación de autocorrelación espacial en la prueba de Moran?
Construyamos el estadístico de Moran para la variable pos_hab usando la estructura espacial llamada mTRUE.est:
spdep::moran.test(covid_zmvm$pos_hab, mTRUE.est)##
## Moran I test under randomisation
##
## data: covid_zmvm$pos_hab
## weights: mTRUE.est
##
## Moran I statistic standard deviate = 8.8625, p-value < 2.2e-16
## alternative hypothesis: greater
## sample estimates:
## Moran I statistic Expectation Variance
## 0.656334129 -0.013333333 0.005709563Del indicador obtenido nos interesan tres elementos, como es usual: la magnitud del coeficiente, su sentido y su significancia estadística. En los resultados que aparecen en tu consola identifica cada uno de ellos y responde:
Ejercicio
¿A cuánto asciende el coeficiente estimado? ¿Podría decirse que es alto o bajo?
¿La relación identificada es positiva o negativa?
Un coeficiente como el obtenido, de 0.656, indica que hay una relación positiva entre los valores de los casos positivos de COVID19 y los valores de los casos positivos por COVID19 en los entornos vecinos (sentido de la asociación), además, podríamos decir que es relativamente alto en la medida en que está más próximo a uno que a cero (magnitud de la relación). Ahora, ¿qué hay con su significancia estadística? ¿Cómo podemos saber que dicho resultado,. el 0.656, no es producto de una coincidencia sino un resultado sistemático o consistente? Para ello, evaluaremos el siguiente juego de hipótesis sobre el índice de Moran:
-
\(Ho: I=0\), es decir, ausencia de autocorrelación o, de forma equivalente, distribución espacial aleatoria.
- \(Ha:I \neq 0\), es decir, presencia de autocorrelación o, de forma equivalente, distribución espacial no aleatoria.
Con la información disponible evaluamos dichas hipótesis. Observa como el p-valor obtenido en extremadamente pequeño (p-value < 2.2e-16); si fijamos un nivel de significancia, \(\alpha=0.05\), se rechaza la hipótesis nula en favor de la hipótesis alternativa, por tanto, la variable no se distribuye de forma aleatoria en el espacio, sino que muestra indicios de autocorrelación espacial positiva relativamente alta (0.656).
Ejercicio
Construya una I de Moran con la estructura espacial dada por la matriz donde queen=FALSE responda:
¿La asociación espacial es positiva o negativa?
¿Consideras que es alta o baja?
¿Dirías que dicha relación es producto del azar o que existe un comportamiento sistemático?
3.4.1 Diagrama de Moran
Una forma creativa de expresar gráficamente la autocorrelación es a través de un diagrama de dispersión cuyo eje \(x\) corresponde a la variable de interés, casos positivos de COVID19 por cada 1 mil habitantes, y el eje \(y\) a su rezago espacial; además, al agregar una recta de ajuste sobre los datos estandarizados lograremos que la pendiente de dicha recta corresponda exactamente al valor de la I de Moran. Una de las características del diagrama de Moran es que se descompone en cuatro cuadrantes, tal como aparece en la figura 3.5.
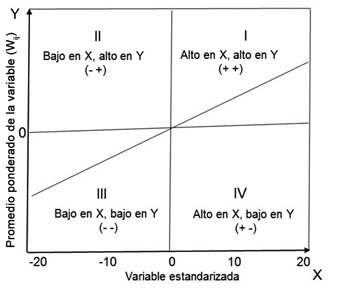
Figura 3.4: Diagrama de dispersión de Moran
Para representar el diagrama de Moran recurrimos a la función moran.plot() del paquete spdep que para una matriz de tipo reina con el argumento queen=TRUE y la base de datos de tipo SpatialPolygonsDataFrame:
spdep::moran.plot(((covid_zmvm$pos_hab)-mean(covid_zmvm$pos_hab))/(sd(covid_zmvm$pos_hab)),
listw = mTRUE.est,
xlab="Casos positivos",
ylab="Rezago espacial de los casos positivos",
main="Diagrama de Moran para casos positivos",
col="lightblue")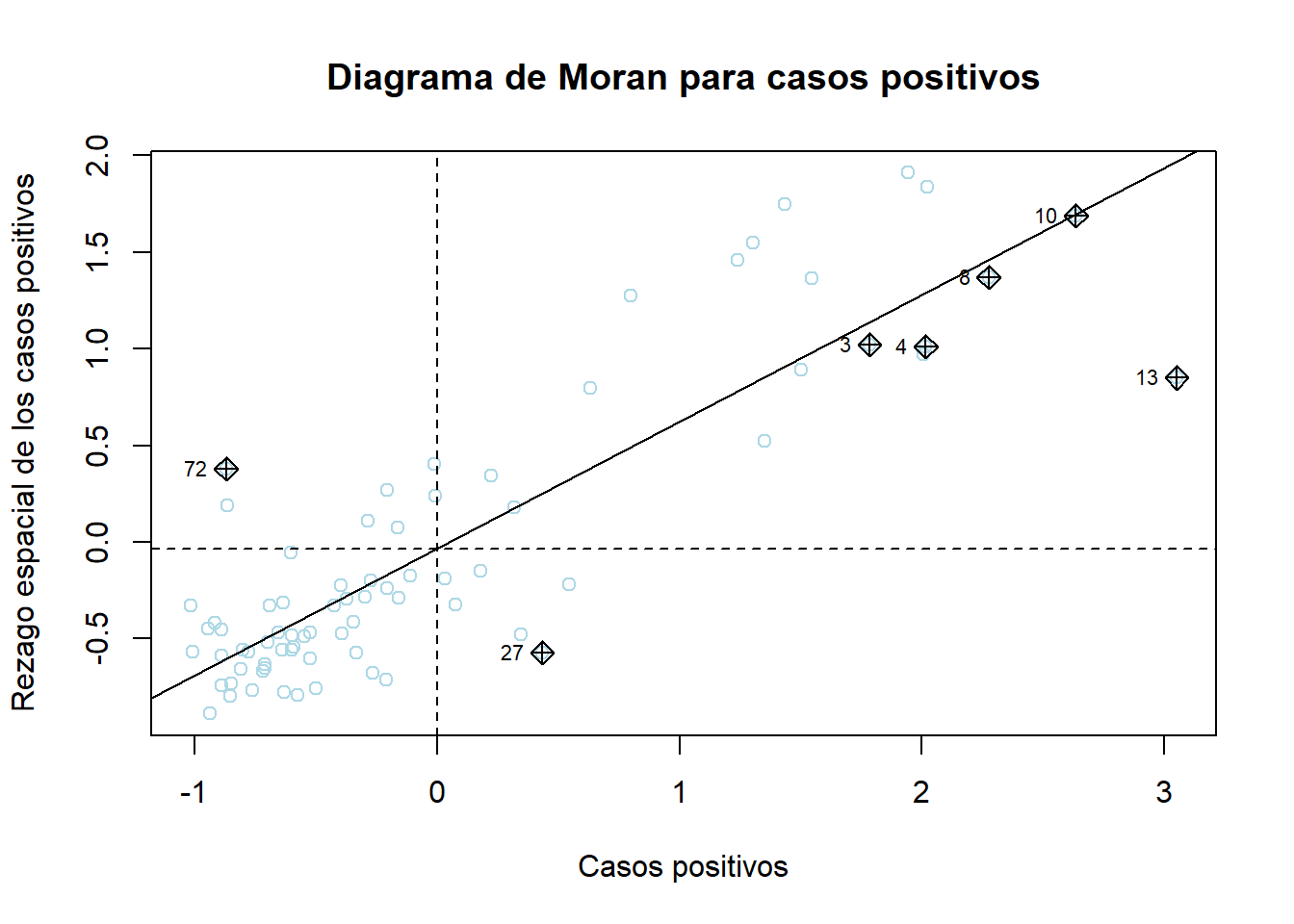
En el diagrama de Moran recién construido notamos varias cosas:
i) Una parte importante de las observaciones caen en el cuadrante I y III, por lo que la relación funcional que predomina entre el conjunto de puntos es positiva.
ii) Que la relación funcional dominante sea positiva no implica que no haya observaciones en los cuadrantes II y IV.
3.5 Múltiples elementos de personalización de ésta y otras gráficas asociadas al paquete base de R pueden revisarse en la documentación de la función par().
Ejercicio
¿Es posible construir un diagrama de Moran usando el paquete ggplot2? De ser así, ¿cómo lo harías?
3.6 Índice de Moran local y mapa de clusters
El índice de Moran que recién hemos calculado permite evaluar la existencia de un patrón espacial completo o global, es decir, para el conjunto de todas las observaciones. Por ello, no proporciona información de la ubicación de las agrupaciones o clusters de alcaldías y municipios. Por ello se dice que la I de Moran es una medida de autocorrelación espacial global: nos dice que hay patrones de concentración o dispersión pero no nos dice a qué municipios o alcaldías específicos es posible atribuir dichas fuerzas de aglomeración.
Para subsanar esta situación, Anselin (1995) propuso la versión local de la I de Moran: el indicador local de asociación espacial o LISA (local indicator of spatial association).
El LISA:
- Proporciona un estadístico para cada ubicación con un nivel de significancia y
- Establece una relación proporcional entre el estadístico local y el global.
Es decir, nos permite identificar a que unidades espaciales (alcaldías o municipios) es posible atribuir la autocorrelación espacial de forma específica y con qué intensidad, en relación con el indicador global. La representación del LISA se hace con arreglo a dos mapas:
- El mapa de cluster o mapa de agrupaciones que permite clasificar las áreas (alcaldías y municipios) con presencia de autocorrelación espacial según el tipo de asociación identificada. Este mapa permite la clasificación de las áreas estadísticamente significativas en clusters o agrupamientos (alto-alto y bajo-bajo) y de áreas que se constituyen como observaciones espaciales atípicas o spatial outliers (agrupamientos bajo-alto y alto-bajo).
- El mapa de significancia: muestra las ubicaciones con la I de Moran local que son representativas en diferentes niveles de significancia.
El Índice local de Moran toma la forma de:
\[I_i = \frac{(x_i-\bar{X})}{S_i^2}{\sum_{j=1,j \neq i}^{n}w_{ij}(x_j-\bar{X})}\] Donde:
\[ S_i^2= \frac{\sum_{j=1,j \neq i}^{n}(x_j-\bar{X}) ^2}{n-1} \] Además, \(x_i\) es el valor de la variable de interés, \(\bar{X}\) es el promedio de dicha variable, \(w_{ij}\) es cada uno de los elementos de la matriz de pesos espaciales y \(n\) es el número de objetos espaciales.
Para calcular un índice de Moran local en R usamos el paquete rgeoda, que es el enfoque más sencillo de ejecutar. Echaremos mano de la función local_moran(), que requiere dos argumentos forzosos: la estructura espacial(w=) y la variable para la que se desea el LISA (df=). Primero, guardemos la variable de la que deseamos un LISA en un objeto independiente:
pos_hab=covid_zmvm_sf["pos_hab"]Luego, usemos dicha variable para construir el LISA:
lisa_poshab <- local_moran(w=queen_w,
df=pos_hab)Dentro del objeto lisa_poshab hay múltiples elementos, que serán útiles más adelante. De momento, llamemos los valores del indicador local de asociación espacial a través de la función lisa_values(), es decir, los valores del índice computado para cada uno de los 76 municipios y alcaldías que componen la ZMVM:
lisaval_poshab <- lisa_values(lisa_poshab)Para representar en un mapa los valores del LISA, es necesario añadirlos a la base de datos original en formato sf:
mapa.lisa <- base::cbind(covid_zmvm_sf, lisaval_poshab)Luego, con las funciones aprendidas en el capítulo anterior, podemos presentar un mapa de quintiles que represente el valor del indicador local de asociación espacial:
tmap::tm_shape(mapa.lisa) +
tmap::tm_fill(col = "lisaval_poshab", style = "quantile",
palette = "Spectral", midpoint= NA,
title = "I de Moran local") +
tmap::tm_borders()
El mapa permite observar la manera en que varía la correlación espacial a nivel local para la variable pos_hab, casos positivos por COVID19 por cada 1 mil habitantes, pues proporciona un valor de correlación para cada municipio y alcaldía: es claro que la mayor parte de los valores altos del LISA se encuentran en la Ciudad de México (tonos en azul).
Necesitamos otros instrumentos que nos permitan identificar si los valores de la I de Moran local son o no significativos, lo que haremos a través del mapa de cluster y su respectivo mapa de significancia. Esto nos permitirá identificar agrupaciones o núcleos de cluster significativos, así como observaciones espaciales atípicas.
Dentro del objeto creado, lisa_poshab, hay múltiples elementos, mismos que pueden ser llamados por funciones específicas, entre las que se encuentran:
-
lisa_clusters(): que los valores de clasificación de cada cluster.
-
lisa_colors(): brinda los colores asociados a cada uno de los clusters computados.
-
lisa_labels(): proporciona las etiquetas de los clusters computados.
Así pues, el mapa los construimos en dos pasos: i) primero obtendremos algunos elementos preliminares para construir el mapa (colores, etiquetas y valores de agrupamiento) y ii) construiremos el mapa con las funciones básicas de R_
#Elementos preliminares
lisa_colores <- lisa_colors(lisa_poshab)
lisa_etiq <- c("No significativo", "Alto-Alto", "Bajo-Bajo", "Bajo-Alto", "Alto-Bajo", "No definido", "Aislado")
lisa_clusters <- lisa_clusters(lisa_poshab)Ahora, con dichos elementos auxiliares, construimos el mapa de cluster:
#Mapa de cluster
plot(st_geometry(covid_zmvm_sf),
col=sapply(lisa_clusters, function(x){return(lisa_colores[[x+1]])}),
border = "#333333", lwd=0.2)
title(main = "Moran Local de pos_hab")
legend('bottomleft', legend = lisa_etiq, fill = lisa_colores, border = "#eeeeee")
Junto con el mapa anterior es común presentar el mapa de significancia, un tipo de representación que indica el nivel de significancia inividual para cada una de las observaciones (municipios y alcaldías). Para ello, también diviimos el procedimiento en dos partes:
#Elementos preliminares
lisa_p <- lisa_pvalues(lisa_poshab)
p_etiq <- c("No significativo", "p <= 0.05", "p <= 0.01", "p <= 0.001")
p_colores <- c("#eeeeee", "#84f576", "#53c53c", "#348124")
#Mapa de significancia
plot(st_geometry(covid_zmvm_sf),
col=sapply(lisa_p, function(x){
if (x <= 0.001) return(p_colores[4])
else if (x <= 0.01) return(p_colores[3])
else if (x <= 0.05) return (p_colores[2])
else return(p_colores[1])
}),
border = "#333333", lwd=0.2)
title(main = "Mapa de significancia de los casos positivos")
legend('bottomleft', legend = p_etiq, fill = p_colores, border = "#eeeeee")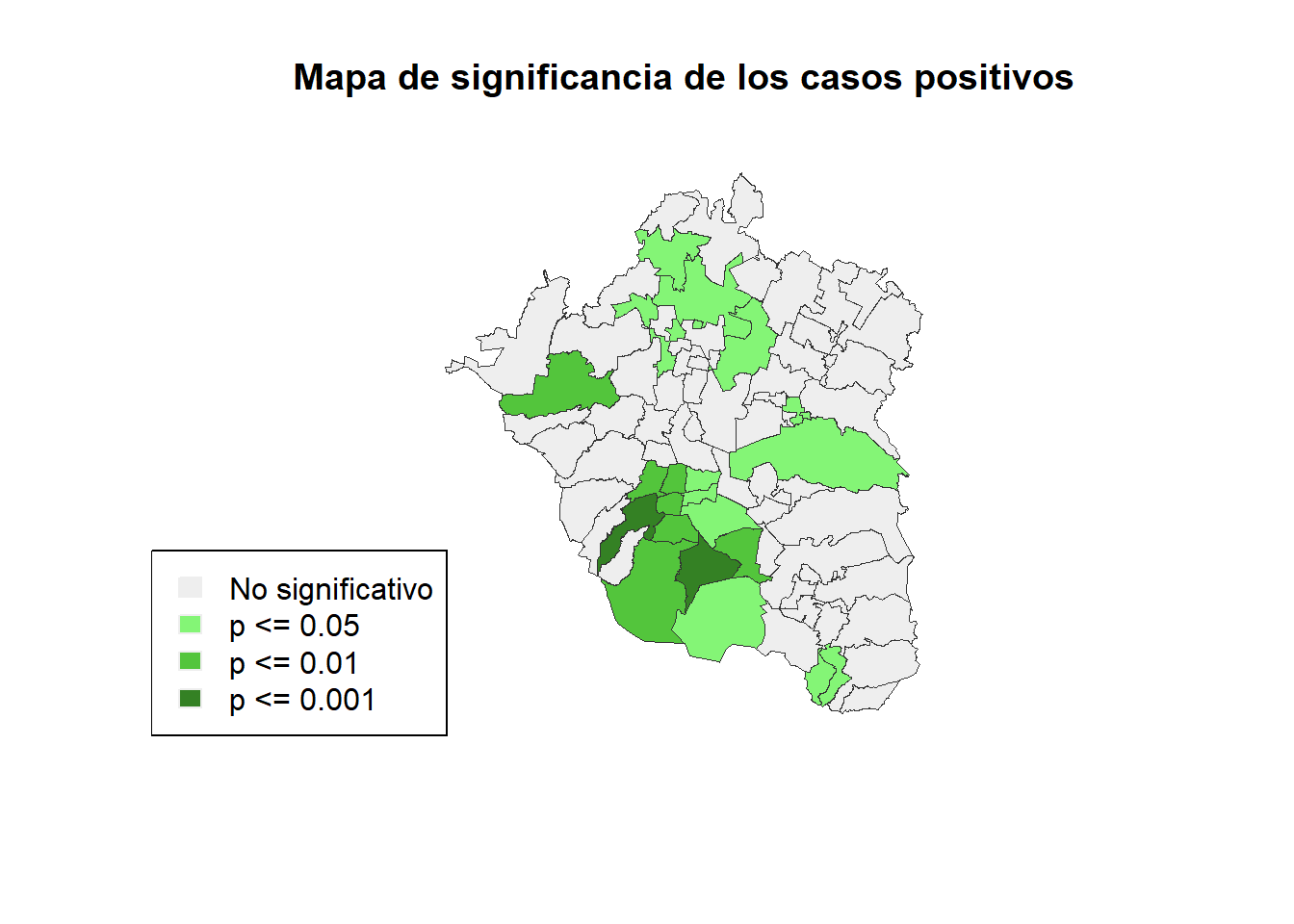
El par de mapas anteriores permiten identificar agrupamientos de valores significativos al 5% o menos, es decid, núcleos de cluster que muestran municipios y alcaldías con valores altos de tasas positivas de COVID19 rodeados de vecinos con valores altos (agrupamiento Alto-Alto), así como agrupamientos de valores bajos (cuadrante Bajo-Bajo), además de observaciones espaciales atípicas (cuadrante Alto-bajo y Bajo-Alto).
En síntesis, hasta este punto hemos visto en este capítulo:
- Cómo definir estructuras de relación espacial a través de diversos criterios,
- Cómo identificar autocorrelación espacial global a través de la I de Moran,
- Cómo evaluar la significancia estadística de la I de Moran,
- Cómo identificar agrupaciones locales a través del indicador LISA.
En el capítulo 5 nos adentraremos en cómo incorporar la riqueza que proporciona el análisis espacial en un modelo econométrico. Mientras tanto, en el capítulo 4 llevaremos a cabo un repaso de elementos básicos sobre los modelos de regresión lineal clásica con mínimos cuadrados ordinarios.